Question

Исследовать сходимость знакопеременных рядов. Если ряд сходится, то определить, сходится он абсолютно или условно.

Answer 1

Сходимость ряда

Признак сходимости знакочередующихся рядов (признак Лейбница):

 Пусть имеется ряд

$\sum\limits_{n=1}^{\infty}a_n$

 Тогда, если выполнены условия:

Ряд является знакочередующимся. Члены ряда убывают по модулю  $\lim\limits_{n\to \infty}|a_n|=0$

то ряд сходится.

1) Чередование знаков

 Ряд является знакочередующимся, т.к. присутствует множитель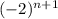 $(-2)^{n+1}$

2) Убывание по модулю

$\lim\limits_{n\to \infty}|\frac{(-2)^{n+1}}{2+3^n} |=\lim\limits_{n\to \infty}\frac{2^{n+1}}{2+3^n}=[\frac{\infty}{\infty} ]$

 Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя

$\lim\limits_{n\to \infty}\frac{2^{n+1}}{2+3^n}=\lim\limits_{n\to \infty}\frac{(2^{n+1})'_}{(2+3^n)'}=\lim\limits_{n\to \infty}\frac{2^{n+1}\cdot ln\,2}{3^n\cdot ln\,3}=\frac{2ln\,2}{ln\,3} \lim\limits_{n\to \infty}\frac{2^n}{3^n}=\frac{2ln\,2}{ln\,3} \lim\limits_{n\to \infty}(\frac{2}{3})^n=0$

 Таким образом, ряд сходится

Тип сходимости

 Сходящийся ряд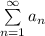  $\sum\limits_{n=1}^{\infty}a_n$ называют абсолютно сходящимся, если сходится ряд $\sum\limits_{n=1}^{\infty}|a_n|$.

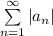 Сходимость такого ряда можно определить с предельного признака Даламбера

$\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}:\frac{2^{n+1}}{2+3^{n}} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}\cdot\frac{2+3^{n}}{2^{n+1}} =2\lim\limits_{n\to \infty}\frac{2+3^{n}}{2+3^{n+1}}=[\frac{\infty}{\infty} ]$

 Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя

$2\lim\limits_{n\to \infty}\frac{2+3^{n}}{2+3^{n+1}}=2\lim\limits_{n\to \infty}\frac{(2+3^{n})'}{(2+3^{n+1})'}=2\lim\limits_{n\to \infty}\frac{3^n\cdot ln\,3}{3^{n+1}\cdot ln\,3} =2\lim\limits_{n\to \infty}\frac{3^n}{3^{n+1}}=\frac{2}{3}$

 Ряд сходится по признаку Вейерштрасса, следовательно исходный ряд сходится абсолютно.