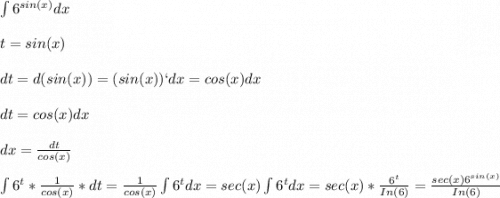
![(\frac{sec(x)6^{sin(x)}}{In(6)})` = \frac{1}{In(6)}(sec(x)6^{sin(x)})` = \frac{1}{In(6)}[(sec(x))`6^{sin(x)} + (6^{sin(x)})`sec(x)] =\\= \frac{1}{In(6)}[tg(x)sec(x)6^{sin(x)} + In(6)cos(x)6^{sin(x)}sec(x)] = = \frac{1}{In(6)}[\frac{6^{sin(x)}sin(x) }{cos^2(x)} + In(6)6^{sin(x)}] = \frac{6^{sin(x)}sin(x) + In(6)6^{sin(x)}cos^2(x) }{In(6)cos^2(x)} = = \frac{6^{sin(x)}sin(x)}{In(6)cos^2(x)} + 6^{sin(x)}](/tpl/images/4506/9654/de656.png)
Нельзя выносить 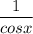 за знак интеграла, т.к. там содержится переменная "х" ... Надо было выразить "х" через "t" и найти dx :
за знак интеграла, т.к. там содержится переменная "х" ... Надо было выразить "х" через "t" и найти dx :
![\displaystyle t=sinx\ \ \Rightarrow \ \ \ x=arcsint\ \ ,\ \ dx=\dfrac{dt}{\sqrt{1-t^2}}\\\\\\\int 6^{sinx}\, dx=\Big[\ t=sinx\ \Big]=\int \frac{6^{t}\cdot dt}{\sqrt{1-t^2}}](/tpl/images/2004/8497/e8664.png)
![\star \ \ \displaystyle \int 6^{sinx}\, cosx\, dx=\Big[\ t=sinx\ ,\ dt=cosx\, dx\ \Big]=\int 6^{t}\, dt=\frac{6^{t}}{ln6}+C=\\\\\\=\frac{6^{sinx}}{ln6}+C\ \ \star](/tpl/images/2004/8497/a55a5.png)
1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)

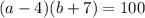


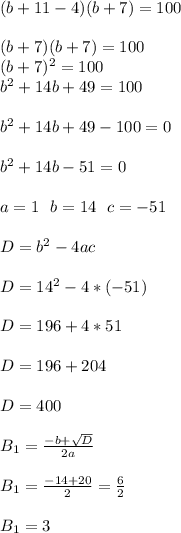
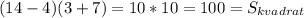
Объяснение:
У 6-му рядку помилково винесено з-під знака інтеграла 1/cos(х). А це зробити не можна , так як х залежить від t і так само від t залежить і 1/cos(х) .