ответ: 1,9 км/ч.
В том случае, если катер будет двигаться против течения реки, его скорость будет равна разнице собственной скорости и скорости течения реки.
Получим:
х - 1,9 км/ч.
Если катер будет двигаться по течению реки, его скорость будет равна сумме собственной скорости и скорости течения реки.
Получим:
х + 1,9 км/ч.
Если подставить вместо значения х любое натуральное число, получим:
х = 10 км/ч.
х - 1,9 = 8,1 км/ч (скорость катера против течения реки ).
10 + 1,9 = 11,9 км/ч (скорость катера по течению реки ).
0,15 (x - 4) = 9,9 - 0,3 (x - 1)
0,15x - 0,6 = 9,9 - 0,3x + 0,3
0,15x + 0,3x = 9,9 + 0,3 + 0,6
0,45x = 10,8
x = 10,8 : 0,45 = 1080 : 45 = 24
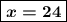
Проверка :
0,15 (24 - 4) = 9,9 - 0,3 (24 - 1)
0,15 · 20 = 9,9 - 0,3 · 23
3 = 9,9 - 6,9 = 3
-----------------------------------------------
1,6 (a - 4) - 0,6 = 3 (0,4a - 7)
1,6a - 6,4 - 0,6 = 1,2a - 21
1,6a - 1,2a = 6,4 + 0,6 - 21
0,4a = -14
a = -14 : 0,4 = - 140 : 4 = -35

Проверка :
1,6 (- 35 - 4) - 0,6 = 3 (0,4 · (-35) - 7)
1,6 · (-39) - 0,6 = 3 · (-14 - 7)
-62,4 - 0,6 = 3 · (-21)
-63 = -63
Объяснение:
Будуємо графіки даних функцій : у = х² - парабола
у = х + 1 - лін. ф-ція , (0 ; 1) , (- 1 ; 0) .
Межі інтегрування знайдемо із сист. рівнянь :
{ у = х²,
{ у = х + 1 ; x² = x + 1 ; x²- x - 1 = 0 ; D = 5 >0 ; x₁ = ( 1 - √ 5)/2; x₂ = ( 1+√ 5)/2;
площу обмеженої графіками фігури знайдемо за формулою :
S = ∫ₐᵇ( x + 1 - x² )dx = ( x²/2 + x - x³/3 )│ₐᵇ = [ 1/2 *((1 + √5)/2 )² + (1 + √5)/2 -
- 1/3 *(( 1 + √5)/2)³ ] - [ 1/2 *((1 -√5)/2 )² + (1 - √5)/2 - 1/3 *(( 1 - √5)/2)³ ] = і т. д.
=