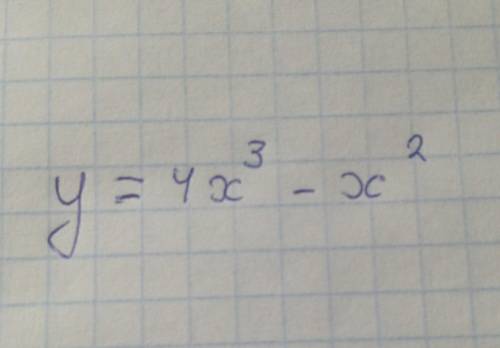
Примем вершину пирамиды в начале координат.
Тогда тогда боковые рёбра равны x, y, z.
Выразим площади боковых граней:
xz = 8,
yz = 16,
xy = 18.
Решим эту систему: z = 8/x. y*(8/x) = 16, отсюда у = 2х. Подставим в 3 уравнение: х * 2х = 18, 2х² = 18 или х = +-√9 = +-3.
Отрицательное значение не принимаем, примем х = 3, тогда у =2*3 = 6, z = 8/3.
Найдём стороны основания по Пифагору.
a = √(3² + 6²) = √(9 +36) = √45 = 3√5.
b = √(3² + (8/3)²) = √(6 +(64/9)) = √(100/9) = 10/3.
c =√(6² + (8/3)²) = √(36 +(64/9)) = √(388/9) = √388/3 ≈ 6,566.
Найдём площадь одной из граней.
So = (1/2)xy = (1/2)*3*6 = 9/
ответ: V = (1/3)SoH = (1/3)*9*(8/3) = 8 куб.ед.
.
Чтобы выяснить,какая из точек не принадлежит графику достаточно координаты этих точек подставить в функцию,которой задан график.
Если получится верное равенство,то точка принадлежит графику, а если неверное, то не принадлежит.
Данная функция прямая, параллельная оси ОХ, вида
у=k*х+b
k=0
k – угловой коэффициент , b – свободный член(-5) , x – независимая переменная.
у=0*х-5
НО
Мы видим , что данная функция не зависит от Х, при любом его значении у=-5 , то есть можно без расчетов найти точку,которая не принадлежит графику. Это точка 3, потому что у=0,а не -5.
Если мы этого не видим,то подставляем:
1) (0: -5)
-5=0*0-5
-5=-5 - принадлежит
2) (-5:-5)
-5=0*-5-5
-5=-5 - принадлежит
3) (-5: 0 )
0=0*-5-5
0≠-5 - не принадлежит
4) (5: -5 )
-5=0*5-5
-5=-5 - принадлежит
чтобы найти промежутки монотонности и точки экстремума, сначала нам нужно найти производную:
y'=12x²-2x
далее приравниваем данное уравнение к нулю и находим нули
12x²-2x=0
2х(6х-1)=0
х=0 и х=1/6
далее ставим точки на координатную прямую и определяем ее знаки на определенных промежутках