1 - В
2 - Г
3 - Д
4 - А
y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=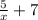
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
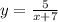, х∈(-∞;-7)∪(-7;+∞) или D=(-∞;-7)∪(-7;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y=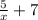 график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: 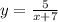то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=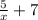, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
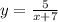, (1вариант) х∈(-∞;-7)∪(-7;+∞) или (2 вариант) D=(-∞;-7)∪(-7;+∞)
1 - В
2 - Г
3 - Д
4 - А
Объяснение:
1) 1,824 : 0,3 - 1,9·0,2 = 6,08 - 0,38 = 5,7
ответ: В
2) 0,2432 : 0,04 - 1,9 · 0,02 = 6,08 - 0,038 = 6,042
ответ: Г
3) 36,48 : 6 + 4,5 · 0,2 = 6,08 + 0,9 = 6,98
ответ: Д
4) 4,864 : 8 + 0,111 · 40 = 0,608 + 4,44 = 5,048
ответ: А
Общий ответ:
1 - В
2 - Г
3 - Д
4 - А