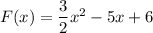\\коэффициент при x^2 равен 1, значит ветки параболы направлены вверх
наименьшее значение находится либо на одном из концов даного отрезка, т.е. у в точке 0 или в т.2 или в вершине параболы т. х=-(a+4)/(2*1)=-a/2-2
y(0)=0^2+(a+4)*0+2a-3=2a-3
y(2)=2^2+(a+4)*2+2a-3=4+2a+8+2a-3=4a+9
y(-a/2-2)=2a-3-(a+4)^2/(4*1)=2a-3-(a^2+8a+16)/4=2a-3-a^2/4-2a-4=-a^2/4-7
если 2а-3=-4
2a=-4+3
2a=-1
a=-1/2=-0.5
y=x^2+(-0.5+4)х+2*(-0.5)-3=x^2+3.5x-4=(x+1.75)^2-7.0625
вершина параболы при а=-0.5 находится в точке х=-1.75, т.е. левее промежутка [0;2], а значит а=-0.5 удовлетворяет условию задачи
если 4a+9=-4
4a=-4-9
4a=-13
a=-13/4=-3.25
y=x^2+(-3.25+4)x+2*(-3.75)-4=x^2+0.75x-11.5=(x+0.375)^2-11.640625
вершина параболы при а=-3.25 находится в точке х=-0.375, т.е левее (не справа) промежутка [0;2], а значит а=-3.25 не удовлетворяет условию задачи (не будет достигатся минимум)
если -a^2/4-7=-4
-a^2/4=-4+7
-a^2/4=3
a^2=-12 - не иммет действительных решений
отвте: -0.5
Объяснение:1.Действия над степенями с целыми показателями выполняются по тем же правилам, что и действия над степенями с натуральными показателями. ( ВЕРНО)
2.Свойства степени с натуральным показателем справедливы и для степени с любым целым показателем, если основание степени не равно нулю. . ( ВЕРНО)
3.Все свойства степени с натуральным показателем справедливы и для степени с любым целым показателем. . ( ВЕРНО)
4.Действия над степенями с целыми показателями не выполняются по тем правилам, по которым выполняются действия над степенями с натуральными показателями.. ( НЕВЕРНО)
Найдём общий вид первообразных:
Найдём константу. Подставим вместо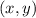
числа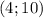 
в уравнение: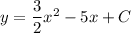
ответ: