1) радиус в точку касания перпендикулярен к касательной)) 2) дуга (отрезанная хордой) связана с центральным углом, опирающимся на эту дугу ---центральный угол определяет градусную меру дуги))) 3) если провести высоту в получившемся равнобедренном треугольнике, то легко вычислить искомый угол... 90°-48°=42°, 90°-42°=48° все это известно как Теорема: Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине градусной меры дуги, заключенной между его сторонами.
Заданное выражение (X^2-5x-6)^1/3 * (x^2-8x+16)<0 надо преобразовать.Выражения в скобках разложить на множитель, приравняв нулю и определив корни. Решаем уравнение x^2-5*x-6=0: Квадратное уравнение, решаем относительно x: Ищем дискриминант:D=(-5)^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49; Дискриминант больше 0, уравнение имеет 2 корня: x_1=(√49-(-5))/(2*1)=(7-(-5))/2=(7+5)/2=12/2=6; x_2=(-√49-(-5))/(2*1)=(-7-(-5))/2=(-7+5)/2=-2/2=-1. Поэтому x^2-5*x-6 = (х - 6)(х + 1). Выражение: x^2-8*x+16 это квадрат выражения : x^2-8*x+16=(х - 4)². Исходное выражение преобразовано в такое: Последнее выражение всегда положительно (оно в квадрате). Кроме значения х = 4. При этом всё выражение превращается в 0. Значит, решает всё первая часть - кубический корень из произведения. Меньше нуля (то есть отрицательным) корень кубический может быть при отрицательном значении подкоренного выражения. Произведение (х - 6)(х + 1) может быть отрицательным при (-1 < x < 6). С учётом того, что из этого промежутка для всего выражения выпадает значение х = 4, то ответ: (-1< x < 4). (4 < x < 6).
Вот конкретные значения заданного неравенства в полученном промежутке: -2 -1 0 1 2 3 4 5 6 7 72 0 -29.074 -19.390 -9.158 -2.289 0 -1.817 0 18
(см. объяснение)
Объяснение:
В своем ответе я приведу два допустимых решения.
1:
Рассмотрим уравнение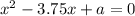 .
.
Пусть y - один из его корней.
Тогда по условию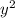 - второй корень уравнения.
- второй корень уравнения.
Итого имеем систему:
Решив ее, получим, что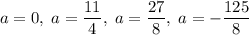 .
.
Проверим теперь каждое значение параметра и выберем те, при которых выполняется решение задачи.
(здесь надо решить 4 уравнения при всех найденных значениях параметра; я этого делать не буду, так как эти действия долгие, но очевидные)
Итого получили, что при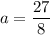 и
и 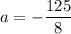 один из корней уравнения
один из корней уравнения 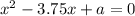 является квадратом другого.
является квадратом другого.
2:
Решим это уравнение через дискриминант:
Выразим корни уравнения:
По условию один из корней должен являться квадратом другого.
Тогда возможны два случая:
Но второй не будет иметь корней, так как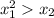 .
.
Запишем единственное уравнение и найдем искомые значения параметра:
Меняем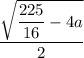 на
на 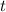 :
:
Откуда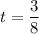 или
или 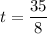 .
.
Обратная замена:
Или:
Итого имеем, что при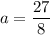 и
и 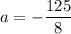 один из корней уравнения
один из корней уравнения 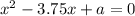 является квадратом другого.
является квадратом другого.
Задание выполнено!