Question

Числа a^2; 3a; a+4 , образуют арифметическую прогрессию.
Найдите ее разность.

Answer 1

2 или - 4

Решение задания прилагаю

Answer 2

Разность арифметической прогрессии:

$\displaystyle d=c_{n+1}-c_n$

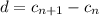
Дано:

$c_1=a^2,\ c_2=3a,\ c_3=a+4$

***********************************

$d=3a-a^2=a+4-3a$

$3a-a^2=a+4-3a\\\\-a^2+3a-a+3a-4=0\\\\-a^2+5a-4=0\ |\ \cdot(-1)\\\\a^2-5a+4=0\\\\D=b^2-4ac=(-5)^2-4\cdot1\cdot4=25-16=9=3^2\\\\a_{1,2}=\dfrac{-b\pm\sqrt{D}}{2a}=\dfrac{5\pm3}{2}\\\\a_1=\dfrac{5-3}{2}=\dfrac{2}{2}=1\\\\a_2=\dfrac{5+3}{2}=\dfrac{8}{2}=4$

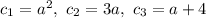
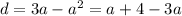
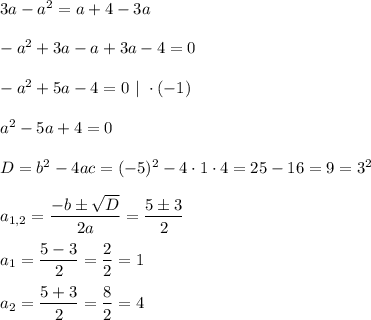
Значит c₁ = a² = 1² = 1, c₂ = 3a = 3 · 1 = 3, c₃ = a + 4 = 1 + 4 = 5 ИЛИ c₁ = a² = 4² = 16, c₂ = 3a = 3 · 4 = 12, c₃ = a + 4 = 4 + 4 = 8.

Тогда d = c₂ - c₁ = 3 - 1 = 2 ИЛИ d = c₂ - c₁ = 12 - 16 = - 4.

ответ: d = 2 или d = - 4.