Question

11 клас алгебра, задачі з параметрами

Answer 1

8. $-\dfrac{125}{8}, \dfrac{27}{8}$

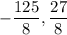
9. 0; 2

Объяснение:

8. Пусть уравнение имеет корни r и r². Тогда по теореме Виета:

$\displaystyle \left \{ {{r+r^2=\dfrac{15}{4}} \atop {r\cdot r^2=a}} \right. \left \{ {{r^2+r-\dfrac{15}{4}=0} \atop {r^3=a}} \right.$

Решим первое уравнение системы:

$4r^2+4r-15=0\\D_{/4}=2^2+4\cdot 15=64=8^2\\r_1=\dfrac{-2+8}{4}=\dfrac{3}{2}\Rightarrow a=\dfrac{27}{8}\\r_2=\dfrac{-2-8}{4}=-\dfrac{5}{2}\Rightarrow a=-\dfrac{125}{8}$

9. Пусть первое уравнение имеет некоторый корень r. Тогда при подстановке числа 3r во второе уравнение левая часть будет равна нулю. Значит, левая часть первого уравнения при r равна левой части второго уравнения при 3r, и обе они равны нулю. Составим систему из первого уравнения и описанного равенства:

$\displaystyle \left \{ {{r^2-3r+a=(3r)^2-5\cdot3r-3a} \atop {r^2-3r+a=0}} \right. \\\left \{ {{8r^2-12r-4a=0} \atop {r^2-3r+a=0}} \right. \\+\left \{ {{2r^2-3r-a=0} \atop {r^2-3r+a=0}} \right. \\3r^2-6r=0\\r=0;2\\a=3r-r^2\Rightarrow a=0;2$