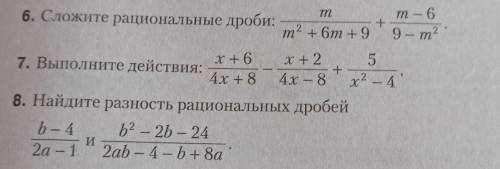
1) Імовірність випадення числа меншого від 5 = 4/6=2/3, бо числа 1 2 3 4 задовольняют умову, а всього на кубику 6 чисел.
Імовірність випадення числа більшого за 4 = 2/6=1/3, бо числа 5 6 задовольняють умову, а всього на кубику 6 чисел.
Для отримання результату помножимо ймовірність виконання умови при першому кидку на ймовірність виконання умови при другому кидку: 2/3*1/3=2/9
2)Імовірність виконнная умови 5/6 при першому кидку і 1/6 при другому. Отримуємо 1/6*5/6=5/36
3)Імовірність випадення на кубику при першому киданні числа більшого ніж при другому киданні дорівнює 1/2-1/6=1/3, оскільки 1/6-імовірність випадення дубля. Наприклад, перший раз випало число 1. Імовірність випадення того самого числа при другому киданні дорівнює 1/6 (6 варіантів 1 з яких нас задовольняє).1/2 ми вказуємо, бо при киданні використовується один і той самий кубик, і кількість випадків, які нас задовольняють удвічі менша за тотальну кількість імовірних подій, тобто імовірність симетрична.
Отже, відповідь: 1/3
Объяснение:
A1.
a) (5a+10)/(b-7):(a²+4a+4)/2b-14=(5(a+2)/(b-7) * ((2(b-7))/(a²+4a+4)=
=(5(a+2)2(b-7))/((b-7)(a+2)²)=5*2/(a+2)=10/(a+2)
a²+4a+4=0; D=16-4*1*4=0
a₁=a₂=0,5(-4±√0)= -2
a²+4a+4=(a+2)(a+2)=(a+2)²;
б) (√50-√6)/√12=(√(25*2)-√(3*2))/(√3*2*2)=(5√2-√(3*2))/(√3*2*2)=
=(5-√3)/√6=(√6(5-√3)/6=(5√(3*2)-√(3*3*2))/6=(5√6-3√2)/6.
A2.
а) (√2)⁶/32=(2¹⁽²)⁶/2⁵=2³/2⁵=2³⁻⁵=2⁻²=1/2²=1/4;
б) (5,2*10⁻⁷)(3,5*10⁴)=5,2*3,5*10⁻⁷⁺⁴=18,2*10⁻³=1/(18,2*10³);
в) 3⁻⁶*9⁻²/(3⁻¹²)=3⁻⁶*(3²)⁻²/3⁻¹²=3⁻⁶*3⁻⁴/3⁻¹²=3⁻¹⁰/3⁻¹²=3⁻¹⁰⁻⁽⁻¹²⁾=3⁻¹⁰⁺¹²=3²=
=9.
А3.
x²+2x=16x-49;
x²+2x-16x+49=0;
x²-14x+49=0;
x²-2*7x+7²=0;
(x-7)²=0;
x₁=x₂=7.
B1.
x³-3x²-4x+12=0;
(x³-3x²)-(4x-12)=0;
x²(x-3)-4(x-3)=0;
(x-3)(x²-4)=0;
x-3=0; x=3;
x²-4=0; x²=4; x=±√4; x=±2;
x₁=-2; x₂=2; x₃=3
1) 18 / (m³ + 3m² - 9m -18)
(или
18 / [ (m² - 9)*(m + 3) ];
18 / (m + 3)²*(m - 3) )
2) (x + 3) / (x² - 4)
3) 2 / (2a - 1)
(или
-2 / (2a - 1);
2 / (1 - 2а)
в случае, если поменять выражения местами)
Объяснение:
1)
m / (m² + 6m+9) + (m -6) / (9 - m²) = m / (m + 3)² + (m -6) / (3 - m)(3 + m) = [ m*(3 - m) + (m -6)*(m + 3) ] / (m + 3)²*(3 - m) = [ 3m - m² + m² - 3m - 18 ] / [ (9 - m²)*(m + 3) ] = -18 / (9m + 18 -m³ - 3m²) = 18 / (m³ + 3m² - 9m -18)
2)
[(x + 6) / (4x + 8)] - [(x + 2) / (4x + 8)] + [5 / (x² - 4)] =
[(x + 6)*(x - 2) - (x + 2)*(x - 2) + 5*4] / [4*(x + 2)*(x - 2)] =
[ x² + 4x -12 - x² + 4 + 20] / [4*(x + 2)*(x - 2)] =
[ 4x + 12] / [4*(x + 2)*(x - 2)] =
[ 4*(x + 3) ] / [4*(x + 2)*(x - 2)] =
(x + 3) / (x² - 4)
3)
[(b - 4) / (2a - 1)] - [(b² -2b - 24) / (2ab - 4 -b + 8a)] =
[(b - 4) / (2a - 1)] - [(b² -2b - 24) / ( 2a*(b + 4) - (b + 4) )] =
[(b - 4) / (2a - 1)] - [(b² -2b - 24) / ( (b + 4)*(2a - 1) )] =
[(b - 4)*(b + 4) - b² +2b + 24] / [(b + 4)*(2a - 1)] =
[ b² - 16 - b² +2b + 24] / [(b + 4)*(2a - 1)] =
[ 2b + 8] / [(b + 4)*(2a - 1)] = [ 2*(b + 4) ] / [(b + 4)*(2a - 1)] =
2 / (2a - 1)