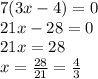
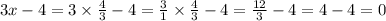
Произведение равно нулю, если хотя бы один из множителей равен нулю
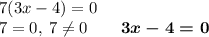
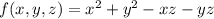
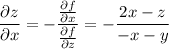
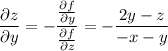
 с координатами
с координатами 
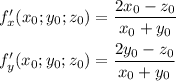
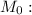
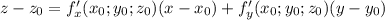 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.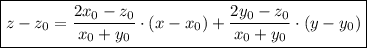 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
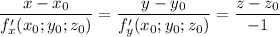
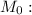
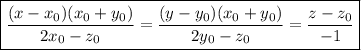 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
Если 7(3x - 4) = 0, то 3x - 4 = 0
Объяснение:
Если 7(3x - 4) = 0, то 3x - 4 = ...
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Выражение 7(3x - 4) состоит из двух множителей: 7 и 3x - 4. Так как 7 ≠ 0, то выходит, что 3x - 4 должно быть равно нулю.