Пусть у Кати х марок, у Павла у марок. Павел отдал Кате х марок, тогда у Кати стало 2х марок, а Павла (у-х) марок. Катя отдала Павлу (у-х) марок, тогда у Павла стало 2(у-х) марок, а у Кати 2х-(у-х)=(3х-у) марок. По условию 2(у-х) марок Павла на 40 больше, чем у него было, т.е. у марок. Составляем первое уравнение 2(у-х)-40=у По условию (3х-у) марок Кати в три раза меньше, чем у нее было,т. е х марок. Составляем второе уравнение х=3(3х-у) Решаем систему двух уравнений: {2(у-х)-40=у ⇒ у = 2х+40 {х=3(3х-у) ⇒ 3у=8х
3(2х+40)=8х 6х+120=8х\2х=120 х=60
у=2х+40=2·60+40=120+40=160 О т в е т. б) 160 марок собрал Павел.
Так как течение реки одинаково действует на обе лодки, то на время их встречи оно не влияет. И, в системе отсчета, связанной с рекой, лодки одинаковое расстояние по 64 км. Скорость лодки в стоячей воде: v = S/t = 64 : 2 = 32 (км/ч) В системе отсчета, связанной с берегом реки, лодки пройдут разное расстояние, так как скорости лодок относительно берега будут различны: скорость лодки, идущей по течению: v₁ = v + v₀ = 32 + 2 = 34 (км/ч) скорость лодки, идущей против течения: v₂ = v - v₀ = 32 - 2 = 30 (км/ч)
Поэтому первая лодка пройдет до места встречи, относительно берега: S₁ = v₁t = 34 * 2 = 68 (км) - по течению Вторая лодка пройдет относительно берега: S₂ = v₂t = 30 * 2 = 60 (км) - против течения
PS. Уточнение "относительно берега" желательно в ответе, поскольку относительно воды лодки равное расстояние. В этом легко убедиться, если в момент старта лодок, на половине расстояния между пристанями, спустить на воду плот. Обе лодки достигнут плота одновременно.
(см. объяснение)
Объяснение:
79:
Выразим из второй строки системы:
из второй строки системы:
Подставим его в первую строку системы:
Берем дискриминант, деленный на четыре, и приравниваем его к нулю:
Итого при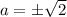 исходная система уравнений имеет ровно одно решение.
исходная система уравнений имеет ровно одно решение.
80:
В первой строке системы имеем график двух параллельных прямых, равноудаленных от прямой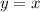 при
при 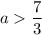 . При
. При  графиком будет прямая
графиком будет прямая
Во второй строке системы имеем уравнение окружности с радиусом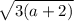 и центром в точке
и центром в точке 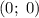 .
.
Тогда, при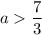 каждая прямая пересекает окружность столько же раз, сколько другая.
каждая прямая пересекает окружность столько же раз, сколько другая.
Очевидно, что сразу возьмем в ответ .
.
Покажем, что случая, когда обе прямые касаются окружности, не существует.
По формуле расстояния от точки до прямой этот случай можно описать так:
Итого при исходная система уравнений имеет ровно два различных решения.
исходная система уравнений имеет ровно два различных решения.
81:
Значение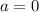 не подходит.
не подходит.
При :
:
Бусконечное число решений будет, если коэффициенты угла наклона и смещения прямых совпадают.
Итого при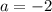 исходная система имеет бесконечное число решений.
исходная система имеет бесконечное число решений.
Задание выполнено!