
x ∈ {arctg(-4)+πn, π/4+πn}, n — целое
Объяснение:
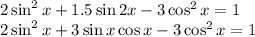
cos x = 0 при x =  . Проверим, является ли этот x корнем. Все углы такого вида на единичной окружности накладываются друг на друга, поэтому примем n = 0:
. Проверим, является ли этот x корнем. Все углы такого вида на единичной окружности накладываются друг на друга, поэтому примем n = 0:
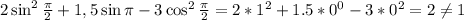
Теперь можно утверждать, что в заданном уравнении cos x и все его степени ненулевые.
Разделим обе части на 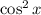 :
:
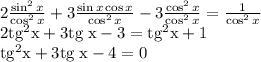
Введем замену 
Имеем:
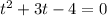
По теореме Виета
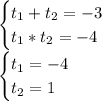
Если t = -4, то
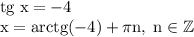
Если t = 1, то
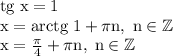
1) да; 2) да; 3) нет; 4) нет
Объяснение:
Нужно подставить в уравнения системы х=2; у=-1
Если получаются верные равенства в обоих уравнениях системы, то пара чисел (2; -1) будет решением системы, если хотя бы одно равенство будет неверно, то пара чисел не будет решением системы.
1) 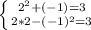
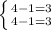 (2; -1) является решением
(2; -1) является решением
2) 
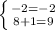 (2; -1) является решением
(2; -1) является решением
3) 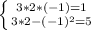
 (2; -1) НЕ является решением, т.к первое равенство неверно.
(2; -1) НЕ является решением, т.к первое равенство неверно.
4) можно не проверять, потому что 3ху=1 уже проверяли в задании 3), получилось неверное равенство, поэтому (2; -1) НЕ является решением
Уравнение 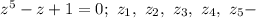 корни этого уравнения.
корни этого уравнения.
Требуется вычислить выражение 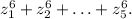 Заметим, что для любого корня уравнения выполнено
Заметим, что для любого корня уравнения выполнено 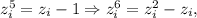
поэтому сумма шестых степеней корней этого уравнения равна сумме вторых степеней минус сумма самих корней.
Теперь вступает в бой волшебник - великая теорема Виета. Вот ее формулировка, записанная в случае, когда старший коэффициент равен одному, а многочлен имеет пятую степень.
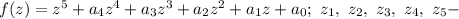 его корни.
его корни.
1) Тогда 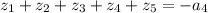 (сумма корней равна коэффициенту при четвертой степени, взятому с обратным знаком). В нашем случае этот коэффициент равен нулю, поэтому сумма корней равна нулю.
(сумма корней равна коэффициенту при четвертой степени, взятому с обратным знаком). В нашем случае этот коэффициент равен нулю, поэтому сумма корней равна нулю.
2) 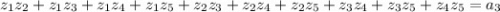 (сумма попарных произведений корней равна коэффициенту при третьей степени). В нашем случае этот коэффициент равен нулю, поэтому сумма попарных произведений корней равна нулю.
(сумма попарных произведений корней равна коэффициенту при третьей степени). В нашем случае этот коэффициент равен нулю, поэтому сумма попарных произведений корней равна нулю.
3) Сумма тройных произведений корней равна  В этой задаче нам это равенство не понадобится.
В этой задаче нам это равенство не понадобится.
4) Сумма четверных произведений равна 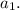 Это тоже нам не понадобится.
Это тоже нам не понадобится.
5) 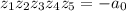 (произведение корней равно свободному члену, взятому с обратным знаком). И это нам не понадобится.
(произведение корней равно свободному члену, взятому с обратным знаком). И это нам не понадобится.
Напоминаю, что мы уже доказали, что сумма корней равна нулю, остается разобраться с суммой квадратов корней. Напрямую теорема Виета ничего про эту сумму не говорит, но дело мастера боится. Имеем:
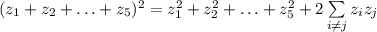
(то есть квадрат суммы равен сумме квадратов плюс удвоенная сумма попарных произведений - элементарное обобщение общеизвестной формулы (a+b)²=a²+b²+2ab). В нашем случае сумма корней и сумма попарных произведений корней равна нулю. Поэтому и сумма квадратов корней равна нулю.
А в общем случаен из теоремы Виета следовало бы, что
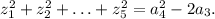
ответ: 0
n принадлежит целым числам
Объяснение:
P.s. cos²(x)≠0 т.к. на ноль делить нельзя
Пусть tg(x) =y,тогда
Вернёмся к замене:
Если tg(x) = 1,тогда
n принадлежит целым числам
Если tg(x) = 4,тогда
n принадлежит целым числам