Question

При каких значениях параметра а уравнение (x+2)|x|=a имеет три корня?

Answer 1

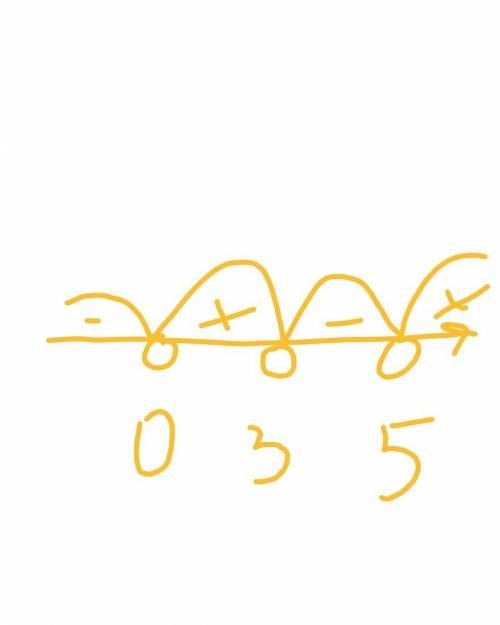
Объяснение:

построим график функции y=(x+2)|xI

1) при х≥0 IxI=x

y=(x+2)x=x²+2x

y=x²+2x

коэффициент при х² положительный ⇒ ветки направлены вверх

y(0)=0;

вершина параболы y=x²+2x в точке х₀=-b/2a=-2/2=-1

y₀=y(x₀)=y(-1)=1-2=-1   (-1;-1)

графиком является часть правой ветки параболы начиная от точки

(0;0)

2)  при х<0

IxI=x

y=(x+2)(-x)=-x²-2x

y=-x²-2x

коэффициент при х² отрицательный  ⇒ ветки направлены вниз

вершина параболы y=-x²-2x в точке х₀=-b/2a=2/(-2)=-1

y₀=y(x₀)=y(-1)=-1+2=1   (-1;1)

графиком является левая ветка параболы и часть правой ветки до точки (0;0)

lim-x²-2x=0

x->0-

в точке (0;0) левая и правая часть графика соединяются

3)

смотрим на чертеж

очевидно, что чтобы уравнение (x+2)|x|=a  имело три корня

прямая y=a должна пересекать график y=(x+2)|x|  в трех точках

это возможно если а будет между 0 и 1

a∈(0;1)