
№1 (а)
ответ: -\frac{4}{3}" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=x%20%3E%20-%5Cfrac%7B4%7D%7B3%7D" title="x > -\frac{4}{3}">
№1 (б)
№2 (а)
-4} \atop {x\leq -2.5}} \right." class="latex-formula" id="TexFormula6" src="https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7Bx%3E-4%7D%20%5Catop%20%7Bx%5Cleq%20-2.5%7D%7D%20%5Cright." title="\left \{ {{x>-4} \atop {x\leq -2.5}} \right.">
№2(б)
\frac{36}{5}" class="latex-formula" id="TexFormula10" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
ответ: \frac{36}{5}" class="latex-formula" id="TexFormula12" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
а)среднее арифметическое равно:
(120+180+110+90+100)/5=600/5=120.
б)Сначало рассчитаем отклонение от нормы.
1. 120-120=0
2. 180-120=60
3. 110-120=-10
4. 90-120=-30
5. 100-120=-20
Дисперсия обозначим её d(Дисперсия множества из N членов находится путем сложения квадратов их отклонений от среднего значения и деления на N).
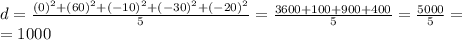
в)Отклонение от значения 60, дисперсия 1000. Исходя из правила получаем.
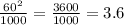
Т.к. 3.6>3.5 то значение 180 ненадёжное(выброс)
г)1.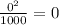 - надёжное.
- надёжное.
2.Ненадёжное. Находили выше.
3.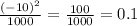 - надёжное.
- надёжное.
4.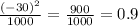 - надёжное.
- надёжное.
5 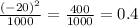 - надёжное.
- надёжное.
Впринципе можно было и не проверять, оно и так понятно)))
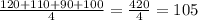
д) Да,т.к. значение 180 мы не учитываем. А среднее арифметическое 4 значение равно 105.
Вродебы так если нигде не ошибся)))
Пусть дан многочлен:
Предположим, что его можно представить в виде произведения многочленов первой степени с действительными коэффициентами.
Многочлен первой степени имеет вид:
Поскольку не содержит свободного члена, то хотя бы один из свободных членов в одном из множителей равен
не содержит свободного члена, то хотя бы один из свободных членов в одном из множителей равен 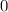 .
.
Но тогда, существует такая линейная комбинация:
При которой данный многочлен тождественно равен .
.
Попробуем найти такую комбинацию:
Мы пришли к противоречию, это невозможно.