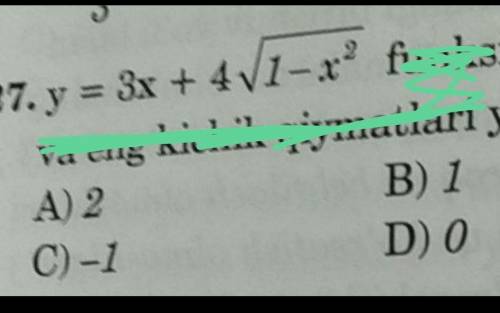
ответ: A) 5-3=2
Объяснение:
приравняв производную к нулю, находим точку экстремума и
определяем вид экстремума (это точка максимума)
т.к. функция ограниченная, то нужно еще смотреть значения функции на концах отрезка области определения функции...
х-марки с птицами, у-марки с машинами . их было поровну,составляем первое уравнение:
х=у
марок с птицами уменьшилось на 5%,Т.Е. ИХ стало х-0,05х, марок с машинами увеличилось на 15%,т.е. из стало у+0,15у. известно, что с машинами на 24 больше, составляем второе уравнение:
у+0.15у=х-0.05х+24
система:
х=у х=у х=у х=у
у+0.15у=х-0.05х+24 1.15у=24+0.95х 1.15х=24+0.95х 1.15х-0.95х=24
х=у х=у
0.2х=24 х=24/0.2=120
пусть скорость лодки в неподвижной воде будет х км/ч
тогда её скорость по течению реки составит (х+1) км/ч, а против течения (х-1) км/ч
время, затраченное на путь против течения реки составит 143/(х-1) часов
время, затраченное на путь по течению реки составит 143/(х+1) часов (обратный путь)
составим уравнение и решим его:
143/(х-1) - 143/(х+1) = 2
143х + 143 - 143х +143 = 2 (х+1)(х-1)
х^2 = 144
x1 = 12 (км/ч) x2 = -12 (не удовл. усл. задачи)
скорость лодки в неподвижной воде 12 км/ч
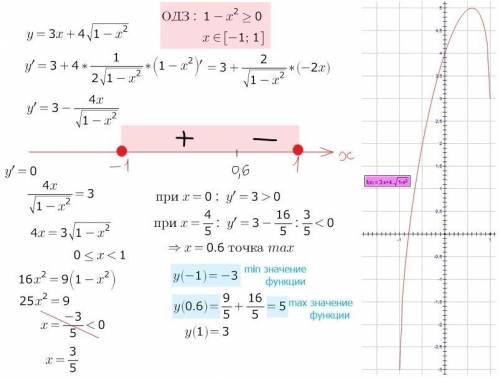
Производная y' = (3х + 4 )' = 3 + 0,5·4 ·(-2x)/
)' = 3 + 0,5·4 ·(-2x)/ = 3 - 4x/
= 3 - 4x/ ;
;
y' = 0 if 3 - 4x/ = 0, (-1 < x < 1) ⇒ 4x = 3
= 0, (-1 < x < 1) ⇒ 4x = 3 ⇔ (обе части
⇔ (обе части
возводим в квадрат при условии x ≥ 0) ⇔ 16х² = 9 - 9х² ⇒ 25х² = 9 ⇒
х₁₂ = ± √9/√25 = ± 3/5. Отрицательный корень откидываем ⇒
х = 3/5 - стационарная точка. При (х = 0,8 > 3/5) y' = 3 - 4*0,8/√0,64 =
3 - 16/3 = - 7/3 < 0 ⇒ х = 3/5 - точка максимума исходной функции, и в ней у принимает наибольшее значение ⇒ Y наиб. = у(3/5) = 9/5 + 4*0,8 = 5; наименьшее значение функции будем искать на концах отрезка [-1; 1]:
y(1) = 3 + 4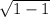 = 3, y(-1) = -3 + 4
= 3, y(-1) = -3 + 4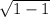 = -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
= -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
Y наиб. + Y наименьшее = -3 + 5 = 2. ответ: А) 2