Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)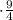 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 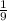 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 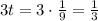 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 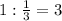 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

[-10, -2]∪[2, 10]
Объяснение:
Перенесём всё в левую часть:
Рассмотрим функцию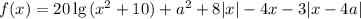 , а также функции
, а также функции 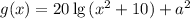 и
и 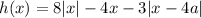 (то есть
(то есть  ).
).
При x ≥ 0 функция g(x) возрастает, так как x² на данном промежутке возрастает, соответственно, прибавив 10, взяв логарифм (возрастающую функцию), умножив на 20 (положительное число) и прибавив a², мы не меняем характер возрастания/убывания функции. Аналогично рассуждая, при x < 0 функция g(x) убывает.
Рассмотрим функцию h(x). При x ≥ 0 . Независимо от того, как раскроется второй модуль, коэффициент перед x будет не меньше единицы, то есть при x ≥ 0 данная функция возрастает, поскольку части этой функции — другие линейные функции с положительным коэффициентом перед x. При x < 0
. Независимо от того, как раскроется второй модуль, коэффициент перед x будет не меньше единицы, то есть при x ≥ 0 данная функция возрастает, поскольку части этой функции — другие линейные функции с положительным коэффициентом перед x. При x < 0  . Аналогично: независимо от того, как раскроется второй модуль, коэффициент перед x будет не больше -9, то есть при x < 0 функция убывает.
. Аналогично: независимо от того, как раскроется второй модуль, коэффициент перед x будет не больше -9, то есть при x < 0 функция убывает.
Таким образом, при x ≥ 0 функция f(x) представляет собой сумму двух возрастающих функций, то есть сама является возрастающей функцией; при x < 0 — сумму двух убывающих функций, то есть сама является убывающей функцией. Значит, минимум функции f(x) достигается в точке x = 0.
Уравнение f(x) = 0 будет иметь корни, если минимум области значений левой части будет не больше нуля. Тогда достаточным условием существования корней является неравенство f(0) ≤ 0: