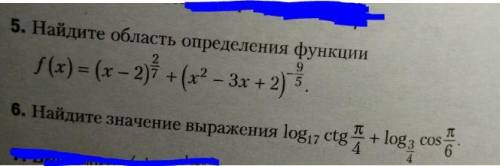
5) Для решения задач подобного типа, нужно знать ограничения (знаменатель не нуль, аргумент логарифма > 0 и т.д.). В данном случаев, если выражение возводится в рациональную степень, то оно >=0
Помним, что:

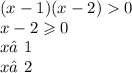
Пересекаем
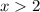
6) Вспомним, что:
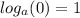

![{x}^{ \frac{m}{n} } = \sqrt[n]{ {x}^{m} }](/tpl/images/2010/2564/ddc57.png)
![|z| = \sqrt[ \alpha ]{ {z}^{ \alpha } }](/tpl/images/2010/2564/6830a.png)
Перепишем выражение:
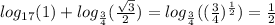
5) Для решения задач подобного типа, нужно знать ограничения (знаменатель не нуль, аргумент логарифма > 0 и т.д.). В данном случаев, если выражение возводится в рациональную степень, то оно >=0
Помним, что:
Пересекаем
6) Вспомним, что:
Перепишем выражение: