
y=kx+b - уравнение прямой с угловым коэффициентом
Подставим в него координаты точек А и В
А (6;-4)
x=6; y=-4
-4=k·6+b
В (8;4)
x=8; y=4
4=k·8+b
Решаем систему двух уравнений и находим k и b:
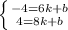

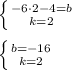
y=2x-16 - уравнение прямой AB с угловым коэффициентом k=2
2x-y-16=0 - общее уравнение прямой АВ
б)
Параллельные прямые имеют одинаковые угловые коэффициенты
y=2x+b - уравнение прямых, параллельных АВ
Чтобы найти прямую, проходящую через точку С подставим координаты точки С
С (-1;6)
6=2·(-1)+b
b=8
y=2x+8 - уравнение прямой, параллельной АВ и проходящей через точку С.
2x-y+8=0 общее уравнение прямой, параллельной АВ и проходящей через точку С.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k₁·k₂=-1
k₁=2
k₂=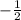 - угловой коэффициент прямой, перпендикулярной АВ
- угловой коэффициент прямой, перпендикулярной АВ
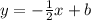 - уравнение прямых, перпендикулярных АВ
- уравнение прямых, перпендикулярных АВ
Подставляем координаты точки С:
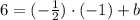
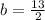
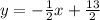 -уравнение прямой, перпендикулярной АВ и проходящей через точку С
-уравнение прямой, перпендикулярной АВ и проходящей через точку С
x+2y-13=0- общее уравнение прямой, перпендикулярной АВ и проходящей через точку С
в)
Прямая, параллельная АВ и проходящей через точку С. пересекается с прямой, перпендикулярной АВ и проходящей через точку С в точке С.
Значит требуется найти точку пересечения прямой АВ и прямой, перпендикулярной АВ и проходящей через точку С
Решаем систему уравнений:
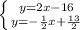
Приравниваем правые части уравнений:
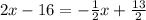
х=9
y=2·9-16
y=2
О т в е т. (9;2)
Объяснение:
у нас по условию есть точки
А(5;8)
В(0; у) - лежит на оси оу
С(1; -4)
из того, что это ромб, мы понимаем, что стороны АВ = ВС
аналогично считаем ВС
и теперь
мы нашли координаты точки В(0;3)
теперь мы можем провести прямую через точки A(5;8) и В(0;3)
мы будем проводить и ещё прямые. я здесь распишу подробно как найти уравнение прямой, проходящей через две точки. дальше буду вывод уравнения опускать. писать только само уравнение
итак, прямая через точки А(5;8) и В(0;3)
мы получили каноническое уравнение прямой
из него легко получить уравнение прямой с угловым коэффициентом:
y = x + 3
теперь мы знаем, что поскольку это ромб, то АВ║CD
тогда уравнение прямой CD (через точки С и D) имеет тот же коэффициент угла наклона (коэффициент при х), что и прямая АВ, т.е. это уравнение вида
у=x+b
и эта прямая проходит через точку С(1; -4), значит координаты точки С должны удовлетворять уравнению прямой. подставим координаты точки С в уравнение
-4 = 1+b ⇒ b = -5
и тогда мы имеем уравнение прямой CD
у = х - 5
аналогично найдем уравнение прямой АD
сначала уравнение прямой ВС (по двум точкам)
у = -7х +3
а потом уравнение ║ ей прямой AD
y = -7x +b она проходит через точку А
8 = (-7)*5+ b b = 43
уравнение прямой AD
y = -7x + 43
теперь мы можем найти координаты точки D как пересечение прямых ВС и CD
x - 5 = -7x +43
8x = 48
x = 6; y = 1
мы нашли координаты точки D(6; 1)
итак, наши точки
А(5;8)
В(0; 3)
С(1;4)
D(6; 1)
теперь уравнение диагонали BD
уравнение прямой, проходящей через две точки
или
ответ
уравнение диагонали BD
точка В(0; 3)
точка D(6; 1)
на графике изображены все прямые и все точки