1. Построить график. Находим вершину параболы. Приводим к виду:
y = x² - 6*x +5 = (x² - 2*x*3 + 3²)-9 +5 = (x-3)² - 4
Получили уравнение ОБЫЧНОЙ ПАРАБОЛЫ ИКС КВАДРАТ, но с вершиной в точке А(3;-4)
Решив уравнение получаем нули функции - х1 = 1 и х2 = 5.
Рисунок с графиком к задаче в приложении.
ответы на вопросы:
1) У(0,5) = 1/4 - 6*0,5 +5 = 2,25 - ответ
2) Y(x) = -1
Решаем квадратное уравнение
x² - 6x - 6 = 0 и получаем: х1 ≈ 1,3 и х2 ≈ 4,7. (с ГРАФИКА).
Интервалы знакопостоянства.
Y>0 - X∈(-∞;-1]∪[5;+∞) - положительна.
Y<0 - X∈[-1;5] - отрицательна.
Внимание - важно. Функция непрерывная - квадратные скобки в написании интервалов у нулей функции.
Решив уравнение получаем нули функции - х1 = 1 и х2 = 5.
4. Возрастает после минимума - Х∈[3; +∞)
и убывает при Х∈(-∞;3]
Объяснение:
незачто!
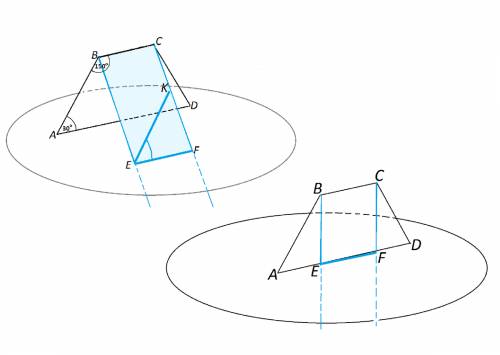
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
Объяснение:
................