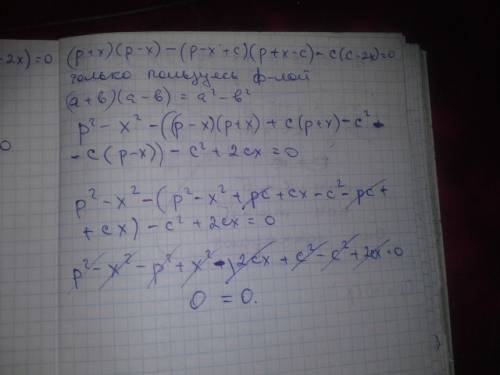
1. а) значение аргумента равно 3, тогда значение функции:
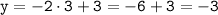
б) Согласно условию значение функции равно 5, то есть,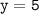 
, то значение аргумента найдем, решив следующее уравнение:
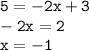
в) Подставляя координаты точки В в график уравнения, получим
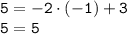
Раз выполняется тождество, следовательно, график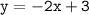 
проходит через точку В(-1;5).
2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: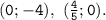 
а) значению аргумента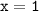 
соответствует значение функции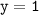 
б) значению функции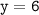 
соответствует значение аргумента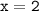 
3. Точки пересечения с осью координат Х. График функции пересекает ось Х при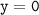 
, значит нужно решить уравнение:
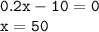
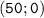- точка пересечения графика с осью ОХ.
Точки пересечения с осью координат У. График пересекает ось У, когда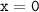 
, то есть, подставляя х=0 в график уравнения, получим
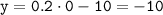
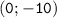- точка пересечения графика с ось ОY.
4. Раз график функции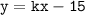 
проходит через точку 
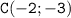, значит значение 
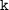найдем, подставив координаты точки C, имеем
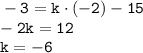
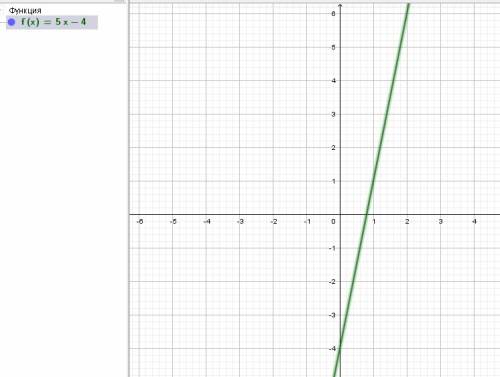
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3
