При каких значениях параметра a уравнение
(5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0 имеет единственное решение
Решение : (5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0
Квадратное уравнение относительно 5ˣ > 0 || t = 5ˣ ||
D = (8a+5)² - 4(16a² +20a -14 )=64a² +80a +25 -64a² -80a+56 =81 =9² >0
т.е. это уравнение всегда имеет 2 решения
1. Если свободный член 16a² +20a - 14 будет отрицательный , то корни будут разных знаков и исходное уравнение будет иметь одно решение .
16a² +20a - 14 = 16(a +7/4)(a - 1/2) < 0 ⇒ a ∈ ( -7/4 ; 1/2 )
- - - - - - -
2. Второй случай свободный член 16a² +20a - 14 = 0
a = -7/4 или a = 1/2
уравнение принимает вид 5ˣ (5ˣ - 8a - 5) = 0, которое будет иметь
очевидно 5ˣ ≠ 0 , остается 5ˣ = 8a + 5 которое имеет решение если 8a + 5 > 0 ⇔ a > - 5 / 8 || a = 1/2 удовлетворяет ||
* * * -7/4 < -5/8 или 8*(-7/4 ) +5 = -14+5 = -9 < 0 * * *
Окончательно ответ: a ∈ ( -7/4 ; 1/2 ]
Мяч брошен с высоты 3 м. На эту высоту он больше не поднимется. Значит значения расстояний, пройденных мячом вниз составляют убывающую геометрическую прогрессию с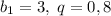 
. Тогда сумма расстояний, пройденных мячом вниз равна сумме всех членов убывающей г.п.
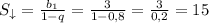метров.
После первого отскока мяч поднимется на высоту 3·0,8 = 2,4 м. Значения расстояний, пройденных мячом вверх составляют убывающую геометрическую прогрессию с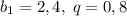 
. Тогда сумма расстояний, пройденных мячом вверх равна сумме всех членов убывающей г.п.
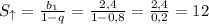метров.
Сумма вертикальных расстояний пройденных мячом вниз и вверх:
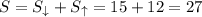метров.
