Пусть х км/ч - собственная скорость лодки, тогда (х + 3) км/ч - скорость лодки по течению реки, (х - 3) км/ч - скорость лодки против течения реки. На путь туда и обратно затрачено 9 часов. Уравнение:
36/(х+3) + 36/(х-3) = 9
36 · (х - 3) + 36 (х + 3) = 9 · (х - 3) · (х + 3)
36х - 108 + 36х + 108 = 9 · (х² - 3²)
36х + 36х = 9х² - 81
72х = 9х² - 81
9х² - 72х - 81 = 0
Разделим обе части уравнения на 9
х² - 8х - 9 = 0
D = b² - 4ac = (-8)² - 4 · 1 · (-9) = 64 + 36 = 100
√D = √100 = 10
х₁ = (8-10)/(2·1) = (-2)/2 = -1 (не подходит, так как < 0)
х₂ = (8+10)/(2·1) = 18/2 = 9
ответ: 9 км/ч - собственная скорость лодки.
Проверка:
36 : (9 + 3) = 36 : 12 = 3 ч - по течению
36 : (9 - 3) = 36 : 6 = 6 ч - против течения
3 ч + 6 ч = 9 ч - туда и обратно
У Толи 18 монет по 2 р. и 5 р. на сумму 97 р.
Если взять 18 монет по 5 р, то общая сумма составит 90 рублей, которая меньше заявленной в условии 97 р. Поэтому с такими данными задача решений не имеет.
Если у Толи 18 монет по 2 р. и 5 р. то сумма денег может быть в пределах от 17·2+5=39 р. до 2+17·5=87 р. с шагом в 3 р.
=================================
В качестве примера решим такую задачу.
У Толи 18 монет по 2 р. и 5 р. на сумму 57 р. Сколько монет каждого достоинства у Толи?
Пусть у Толи х монет по 2 р. и у монет по 5 р. Тогда система :
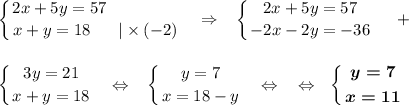
ответ при таком условии : 11 монет по 2 р. и 7 монет по 5 р.
В решении.
Объяснение:
Решите неравенства. Соотнесите свои ответы с названиями промежутков.
1) х²+2х+10 ˃ 0;
Приравнять к нулю и решить квадратное уравнение:
х² + 2х + 10 = 0
D=b²-4ac =4 - 40 = -36
D < 0
Уравнение не имеет действительных корней.
Значит, неравенство выполняется всегда или не выполняется никогда.
Подставить в неравенство произвольное значение х:
х = 0;
0 + 0 + 10 > 0, выполняется.
Значит, неравенство верно при любом значении х.
Решение неравенства х∈(-∞; +∞). ответ b).
2) х² -12х+36 ≤ 0;
Приравнять к нулю и решить квадратное уравнение:
х² - 12х + 36 = 0
D=b²-4ac =144 - 144 = 0 √D=0
х₁,₂=(-b±√D)/2a
х₁,₂=(12±0)/2
х₁,₂=6.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, парабола "стоит" на оси Ох.
Решение неравенства x={5}. ответ c). Скобка фигурная.
3) х²+3х+2 ≥ 0;
Приравнять к нулю и решить квадратное уравнение:
х² + 3х + 2 = 0
D=b²-4ac =9 - 8 = 1 √D=1
х₁=(-b-√D)/2a
х₁=(-3-1)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(-3+1)/2
х₂= -2/2
х₂= -1.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох при х = -2 и х = -1.
Решение неравенства: х∈(-∞; -2]∪[-1; + ∞). ответ f.
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
4) х² - 9 ≤ 0;
Приравнять к нулю и решить квадратное уравнение:
х² - 9 = 0 неполное квадратное уравнение
х² = 9
х = ±√9
х₁ = -3;
х₂ = 3.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох при х = -3 и х = 3.
Решение неравенства: х∈[-3; 3]. ответ d).
a) Неравенство не имеет решений
b) Решением неравенства является вся числовая прямая
c) Решением неравенства является одна точка.
d) Решением неравенства является закрытый промежуток.
e) Решением неравенства является открытый промежуток.
f) Решением неравенства является объединение двух промежутков.
Відповідь:
Пояснення:
Незнаю