7 класс 1. Точки N и M – середины параллельных сторон AD и BC четырехугольника АВСD
соответственно. Докажите, что если МА – биссектриса угла BMN, то MD – биссектриса угла
CMN.
2. В начале на доске записано число 2019. Каждым ходом число можно уменьшить на
любую из его ненулевых цифр (например, из 2019 можно получить: 2019 – 2 = 2017, 2019 –
1 = 2018 или 2019 – 9 = 2010). Петя и Вася ходят по очереди, начинает Петя. Кто из них
сможет выиграть, как бы ни играл соперник, если побеждает тот, кто после своего хода
получит 0?
3. Из чисел от 0 до n выбрали двенадцать и расставили по кругу. Оказалось, что разность
любых двух не соседних чисел делится на количество чисел между ними (количество
чисел считается в том направлении, в котором их меньше). Найдите наименьшее
возможное n.
4. В компании 100 человек, причём каждый из них знаком с 50 членами компании. Известно,
что нет троих, попарно знакомых друг с другом (то есть если X знаком с Y, а Y знаком с Z, то
Z не знаком с X). Докажите, что не найдется пятерых из них A, B, C, D и E , знакомых по
кругу (A c B, B c C, C c D, D c E, E c А).
можно ответ хотя-бы на 1 вопрос
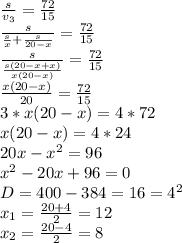
3/(2^(2 - x²) -1)² - 4/(2^(2- x²) -1) + 1 ≥ 0 ;
замена : t = 2^(2-x²) -1
3 / t² - 4 / t +1 ≥ 0 ;
(t² - 4t +3) / t² ≥ 0
для квадратного трехчлена t² - 4t +3 t₁=1 корень: 1² - 4*1+3 = 1- 4+3 =0.
t₂ =3/t₁=3/1=1 (или t₂ =4 -1=3)
* * * наконец можно и решить уравнение t² - 4t +3=0 * * *
(t² - 4t +3) / t² ≥ 0 ⇔ (t -1)(t - 3) / t² ≥ 0 .
+ + - +
(0) [1] [ 3]
* * * совокупность неравенств [ { t ≤ 1 ; t ≠0 . { t ≥ 3 * * *
a)
{ 2^(2-x²) -1 ≤ 1 ; 2^(2-x²) -1 ≠ 0 .⇔ { 2^(2-x²) ≤ 2 ; 2^(2-x²) ≠ 1 . ⇔
{ 2^(2-x²) ≤ 2¹ ; 2^(2-x²) ≠ 2⁰.⇔ {2-x² ≤ 1 ; 2 - x² ≠ 0.⇔{ x² -1 ≥ 0 ; x² ≠ 2⇔
{ (x+1)(x-1) ≥ 0 ; x ≠ ±√2 . ⇒ x∈ ( -∞ ; -√2 ) ∪ (-√2 ; -1] ∪ [1 ; √2) U (√2 ; ∞) .
b)
2^(2-x²) -1 ≥ 3 ⇔ 2^(2-x²) ≥ 4 ⇔2^(2-x²) ≥ 2² ⇔2- x² ≥ 2 ⇔ x² ≤ 0 ⇒ x=0.
ответ: x∈ ( -∞ ; -√2 ) ∪ (-√2 ; -1] ∪ { 0} ∪ [1 ; √2) U (√2 ; ∞) .