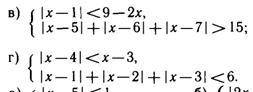
f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
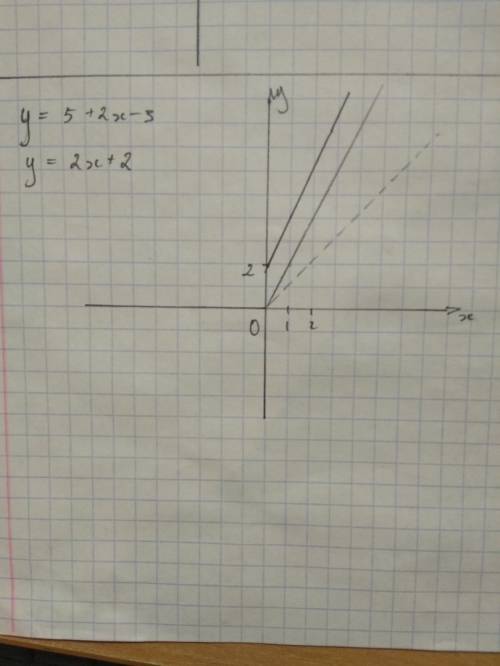
f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
|x - 1| < 9 - 2x
|x - 5| + |x - 6| + |x - 7| > 15
|f(x)| < g(x) ⇒ -g(x) < f(x) < g(x)
2x -9 < x - 1 < 9 - 2x
2x - 9 < x - 1
x < 8
x - 1 < 9 - 2x
3x < 10
x < 10/3
x ∈ (-∞, 10/3)
при таких х модули во втором раскрываются 5 - x, 6 - x, 7 - x
5 - x + 6 - x + 7 - x > 15
18 - 3x > 15
3x < 3
x < 1
Пересекаем ответы
x ∈ (-∞, 1)
г аналогично
Сначала первое потом модули сами во втором раскроются