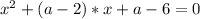
1.
а) 3b+(5a–7b) = 3b+5a–7b = 5a–4b
б) –(8c–4) +4 = –8c+4+4 = 8–8c
в) (2+3x) +(7x–2) = 2+3x+7x–2 = 10x
г) 3(8m–4)+6m = 3×8m–3×4+6m=24m–12+6m=30m–12
д) 15–5(1–a)–6a = 15–5–5a–6a= 10–11a
е) (2a–7y)–(5a–7) = 2a–7y–5a+7 = –3a–7y±7
ж) 14b–(15b+y)–(y+10b) = 14b–15b–y–y–10b = –11b–2y
з) 7(5a+8)–11a–58 = 7×5a+7×8–11a–58 = 35a+56–11a–58 = 24a–2
и) 9x+3(15–8x)–35 = 9x+3×15–3×8x–35 = 9x+45–24x–35 = 10–15x
к) 33–8(11b–1) –2b = 33–8×11b–8–2b = 33–88b–8–2b = 25–90b
2.
а) 0,7b+0,3(b–5) = 0,7b+0,3b–0,3×5 = b–1,5 = –0,81–1,5 = –2,31
б) (y–7)–(14–y) = y–7–14+y = 2y–21 = –0,6–21= –21,6
Объяснение:
Алгебра мой конёк)
Надеюсь
ответ:Скорость реки: 1 км/ч,
Скорость катера: 19 км/ч
Объяснение:
Скорость катера по течению за 15 мин= 5÷0,25(15 мин = 0,25 ч) =20 км/ч. Находим время за которое катер проходит 15 км по течению: 15÷20=0,75 ч. Общее время: 1+45÷60=1,75 ч. Значит, время против течения: 1,75-0,75=1. Находим скорость катера против течения реки: 18÷1=18км/ч. Далее мы берём скорость реки за Х. У нас получается уравнение:
20(км/ч) - 18(км/ч)=2Х
2=2Х
Х=1(км/ч)
Через скорость реки можно найти скорость катера 2-мя
1)20-1=19
2)18+1=19
Остается только оформить задачу как просит Ваш учитель.
Удачи)))
Согласно определению противоположных чисел, два числа будут являться противоположными, если после прибавления одного числа к другому в результате получится ноль.
Для нахождения параметра а воспользуемся теоремой Виета.
Согласно этой теореме сумма корней данного уравнения x^2 + (a - 2)x + a - 6 = 0 равна -(а - 2).
Следовательно, для того, чтобы корни данного уравнения были противоположными числами необходимо, чтобы выполнялось условие:
-(а - 2) = 0,
откуда следует:
а = 2.
Проверим, имеет ли уравнение x^2 + (a - 2)x + a - 6 = 0 корни при а = 2.
Подставляя данное значение параметра а в уравнение, получаем:
x^2 + (2 - 2)x + 2 - 6 = 0;
x^2 - 4 = 0;
(х - 2) * (х + 2) = 0;
х1 = 2;
х2 = -2.
Таким образом, корни данного уравнения являются противоположными числами при а = 2.
ответ: при а = 2.