Испытание состоит в том, что два раза подряд бросают игральный кубик.
Число исходов испытания
n=6·6=36
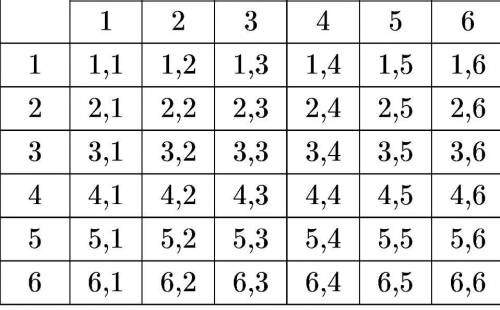
Результаты можно изобразить в виде таблицы:
( см. рис.1)
Первая цифра -число очков, выпавшее на первом кубике,
вторая цифра - число очков, выпавшее на первом кубике.
Получаем 36 двузначных чисел:
от 11 до 16; от 21 до 26; ... от 61 до 66.
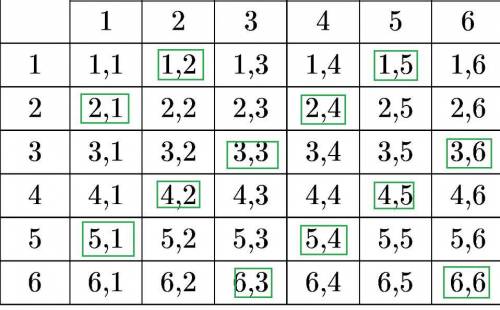
Событие A-"результатом двух последовательных бросков игрального кубика будет число, кратное трем"
m=12 ( cм. рис. 2)
это двузначные числа:
12;15; 21;24;33;36;42;45;51;54;63;66
По формуле классической вероятности
p(A)=m/n=12/36=1/3
57
Объяснение:
Докажем, что среди написанных чисел есть одинаковые.
Действительно, если все написанные числа разные, то различных
попарных сумм должно быть не менее четырёх, например, суммы
одного числа с четырьмя остальными. Значит, среди попарных сумм
есть суммы двух одинаковых натуральных чисел. Такая сумма
должна быть чётной, в нашем списке это число 80. Отсюда следует,
что на доске есть число 40 и оно написано не меньше двух раз.
Пар равных чисел, отличных от 40, на доске быть не может, иначе
среди попарных сумм было бы ещё одно чётное число. Обозначим одно из трёх оставшихся чисел через х, тогда среди
попарных сумм есть число 40 , + х значит, х равно либо 97 40 57, − =
либо 63 40 23. − =
Наборы 40, 40, 40, 40, 57 и 40, 40, 40, 40, 23 нам не подходят, так как
в них всего две попарные суммы. Значит на доске написан набор 40,
40, 40, 57, 23. Таким образом, наибольшее число на доске — это 57.
Представим что Х это хвойные
Следовательно 671-Х = лиственные
Х-1,2=Х2
И в итоге лиственных: Х1
Хвойных: Х2