Общий анализ ребуса–равенства кока + кола = вода позволяет написать неравенства 1 ≤ к ≤ 4 (во-первых, к ≠ 0 как значащая цифра четырёхзначного числа; во-вторых, при к ≥ 5, результат сложения двух четырёхзначных чисел окажется пятизначным, что не возможно: «вода» – четырёхзначное число). Следовательно, в = 2 * к + 1, то есть в ϵ {3; 5; 7; 9}.
Заметим, что разряды единиц слагаемых и суммы выражены одной буквой «а». Однозначно, а = 0, так как все остальные цифры не удовлетворяют равенству а + а = а (даже с учётом перехода десятка на следующий разряд).
Такую же картину наблюдаем в разрядах сотен; однако, здесь ситуация отличается от той ситуации, которую только что рассмотрели. Теперь буква «о», по условию задания, не может быть 0 (разные буквы заменяют разные цифры). Здесь равенству о + о = о с учётом перехода ста (как результат сложения «к» десятков и «л» десятков) на следующий разряд удовлетворяет только о = 9. Следовательно: к + л ≥ 10; в ϵ {3; 5; 7} (цифру 9 исключили, поскольку она уже занята) и к ≠ 4 (иначе, буква «в» приняла бы значение 9, что не возможно).
Неравенство к + л ≥ 10 не позволяет букве «к» принимать значение 1, так как л – однозначное число и л ≠ 9.
Пусть к = 2, тогда 2 + л ≥ 10 или л ≥ 8, откуда л = 8 (так как о = 9). Следовательно, к + л = 10. Тогда, д = 0, что также невозможно, так как а = 0.
Осталось только к = 3. Теперь всё становится на своё место: в = 2 * 3 + 1 = 7; к + л = 3 + л ≥ 10 или л ≥ 7, откуда л = 8 (так как 7 и 9 уже заняты).
Таким образом, ребус «кока + кола = вода» разгадан: 3930 + 3980 = 7910.
ответ: 3930 + 3980 = 7910.
Объяснение:
Введем векторы АВ, BС и АС:
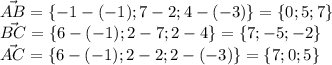
Найдем длины всех сторон треугольника:
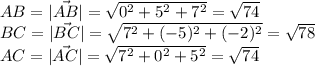
Стороны AB и AC равны, поэтому треугольник - равнобедренный
Учитывая, что треугольник равнобедренный, тупым углом между оказаться только угол, противолежалий основанию, то есть угол А.
Рассмотрим скалярное произведение векторов АВ и АС. С одной стороны скалярное произведение векторов равно сумме попарных произведений их координат:

С другой стороны, скалярное произведение векторов равно произведению их модулей на косинус угла между ними:
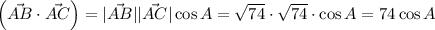
Приравняв два выражения, можно получить значение для косинуса угла между векторами:
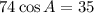
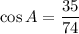
Так как косинус угла А положителен, то угол А острый.
Два других угла В и С не могут быть тупыми, так как они равны, а в треугольнке не можут быть более одного тупого угла.
ответ: треугольник равнобедренный, остроугольный