Пусть х учеников изучают только английский, у - только французский и z - и английский, и французски. Получаем, что ангийский изучают (х+z) учеников, а французский (y+z). Получаем систему из двух уравнений с тремя неизвестными. (x+z)/5=z (y+z)/7=z Отуда получаем x+z=5z y+z=7z
x=4z y=6z Всего в классе учеников x+y+z=4z+6z+z=11z z - натуральное число Так как в классе занято более 30 мест, то 11z>30 Так как в классе 20 двухместных парт, то 11z≤40 Получаем 30 <11z≤40 30/11 < z≤ 40/11 2,7 < z ≤ 3,6 z=3 В классе 33 ученика, 12 из них изучают только английский, 18 -только французский и 3 изучают оба языка
Скорость 1-ой лодки по течению = (х + 4) км/ч Скорость 2-ой лодки против течения = (х - 4) км/ч Скорость сближения лодок = х + 4 + х - 4 = 2х Составим уравнение: 2х * 2,9 = 116 5,8х = 116 х = 20 ответ 1): 20 км/ч - скорость лодки в стоячей воде (собственная скорость каждой лодки)
20 + 4 = 24 (км/ч) - скорость 1-ой лодки по течению 24 * 2,9 = 69,6 (км ая лодка до места встречи.
20 - 4 = 16 (км/ч) - скорость 2-ой лодки против течения. 16 * 2,9 = 46,4 (км ая лодка до места встречи.
1)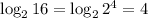
Если в задании опечатка : вместо 0,4 должно быть 0,04
================================
Использованы формулы