Здраствуйте,решите линейное уравнение. 5(х-2)-3(х+1)=6х

Я не могу понять уравнения,сколько бы тем и видео уроков не смотрела ,если можно с объяснениями,последняя надежда что тут.

👇

Увидеть ответ

Ответ:

ксениякейт

11.01.2022

по моему это так если не правильно прости

Здраствуйте,решите линейное уравнение. 5(х-2)-3(х+1)=6х Я не могу понять уравнения,сколько бы тем и

4,4(87 оценок)

Ответ:

DimaNewPARK

11.01.2022

для начала раскрываешь скобки.

5(х-2)-3(х+1)=6х

5х-10-3х-3=6х.

- на - всегда будет +

- на + будет -

+ на - будет -

+ на + будет +

так вот, после раскрытия скобок

считаем дальше

5х-3х= 2х

-10-3=-13

осталось ещё 6х, его мы переносим на другую часть, соответственно меняется его знак. то есть 6х=как+6х, если переносим, то знак меняется и становится -6х

получается

2х-6х=13 (заметь, было -13, но из-за того, что перенесли на другую часть, его знак поменялся, и стал +13

считаем

-4х=13

х=13:(-4)=-3,25

ответ: х=-3,25

4,6(53 оценок)

Открыть все ответы

Ответ:

alicemuhametp0aof9

11.01.2022

В обеих точках функция непрерывна

Объяснение:

Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.

для x = 0

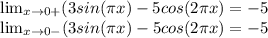
$\lim_{x \to 0+} (3sin(\pi x) - 5cos(2\pi x) = -5\\ \lim_{x \to 0-} (3sin(\pi x) - 5cos(2\pi x) = -5$

Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна

для x = 1

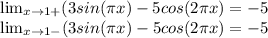
$\lim_{x \to 1+} (3sin(\pi x) - 5cos(2\pi x) = -5\\ \lim_{x \to 1-} (3sin(\pi x) - 5cos(2\pi x) = -5$

Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.

4,4(8 оценок)

Ответ:

Danfdffefd

11.01.2022

Исходное неравенство распадается на совокупность систем:

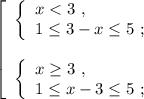
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

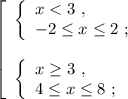
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

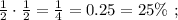
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

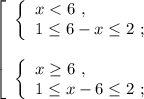
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

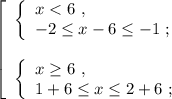
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

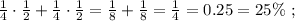
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...

Образование

05.08.2020

Решить систему уравнений x2 + xy +y2 = 13...

Образование