1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
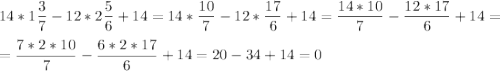
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
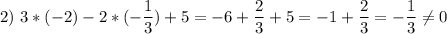
не является решением
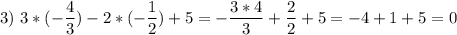
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
D = 81-768=- 687
действительных корней нет
1) 4y^2 - 25y + 100=0
D = 625-1600, D<0 действительных корней нет
3) из условия знаменателя: х не равен -3 и 1/2. Далее по условию равенства нулю дроби:
(x+3)(x-2)=0
x+3=0 или x-2=0
x=-3 x=2
ответ: 2 (так как -3 не подходит по условию знаменателя)
4) Приведем к общему знаменателю:
(16(x^2-9)+x^2(x-6)-x^2(x+3))/(x^2(x^2-9)) = 0
x не равен 0, 3 и - 3
16(x^2-9)+x^2(x-6)-x^2(x+3)=0
16x^2-144+x^3-6x^2-x^3-3x^2=0
7x^2=144
x1=12/√7
x2=- 12/√7