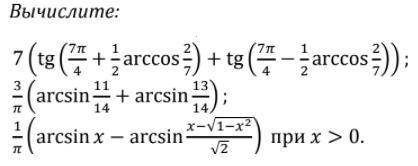
ответ: 1) (-4; -1.5) U (¹/₃; +oo) 2) (-oo; -1) U (2; 4)
Объяснение:
подобные неравенства решаются методом интервалов))
что при умножении, что при делении правила получения знака результата одинаковы:
"+" на "+" будет "+";
"-" на "+" будет "-";
"-" на "-" будет "+"... потому решения этих неравенств очень похожи))
главное --найти корни для каждого множителя/делителя или делимого
(2x+3)(3x-1)(x+4) > 0
корни: -1.5; ¹/₃; -4... определяем знак на крайнем правом промежутке (на +бесконечности) --будет "+" и при переходе через корень функция меняет знак (кратных корней нет)
---------(-4)++++++++(-1.5)---------(¹/₃)+++++++
ответ: (-4; -1.5) U (¹/₃; +oo)
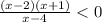
корни: 2; -1; 4... определяем знак на крайнем правом промежутке (на +бесконечности) --будет "+" и при переходе через корень функция меняет знак (кратных корней нет)
---------(-1)++++++++(2)---------(4)+++++++
ответ: (-oo; -1) U (2; 4)
ответ: -49
ответ: 2
x\in (0;1]⇒![\frac{x-\sqrt{1-x^2}}{\sqrt{2}}\in[-1;1].](/tpl/images/2023/4007/af1fa.png) Рассмотрим
Рассмотрим ![a\in [0;\frac{\pi}{2}]](/tpl/images/2023/4007/04d08.png) (
(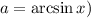 такой, что
такой, что
Поскольку![a-\frac{\pi}{4}\in [-\frac{\pi}{2};\frac{\pi}{2}]\Rightarrow \arcsin (\sin(a-\frac{\pi}{4}))=a-\frac{\pi}{4}=\arcsin x-\frac{\pi}{4}.](/tpl/images/2023/4007/69d6b.png)
ответ: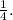
Замечание. Мы использовали формулы