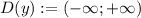
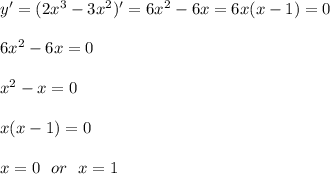
![+++++++[0]---------[1]+++++++\ \textgreater \ x](/tpl/images/0905/2672/fbfbf.png)
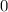являеться максимумом функции 
,
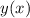являеться минимумом функции 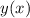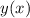монотонно растет на промежутке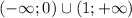 
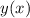монотонно убывает на промежутке 
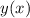пересекает ось ОХ в точкаx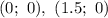 
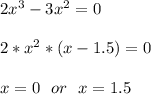
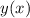пересекает ось ОУ в точке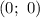 
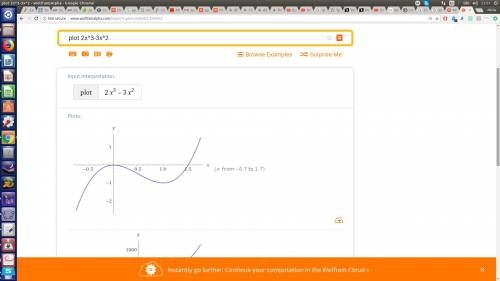
По условию имеем:
a₁+a₅=26
a₂*a₄=160
Распишем 2й, 4й и 5й члены прогрессии через a₁:
a₂=a₁+d
a₄=a₁+3d
a₅=a₁+4d
Выполним подстановку в первое равенство:
a₁+(a₁+4d)=26
2a₁+4d=26
упростим, т.е. разделим обе части равенства на 2:
a₁+2d=13
Далее, выполним подстановку во второе равенство:
(a₁+d)*(a₁+3d)=160
Для сокращения расчетов во второй скобке распишем выражение:
(a₁+d)*((a₁+2d)+d)=160
Из первого равенства было получено, что a₁+2d=13. Подставим это значение во вторую скобку, получим:
(a₁+d)*(13+d)=160
Выразим a₁ из первого равенства:
a₁=13-2d и подставим в последнее равенство:
(13-2d+d)*(13+d)=160
(13-d)(13+d)=160
Произведение в левой части равенства свернем по формуле разности квадратов:
13²-d²=160
169-d²=160
d²=9
d=3
a₁=13-2d
a₁=13-2*3
a₁=13-6
a₁=7
Далее по формуле суммы первых n членов прогрессии находим:
Sn=(2*a₁+(n-1)*d)/2*n
S₆=(2*7+5*3)/2*6
S₆=(14+15)/2*6
S₆=29/2*6
S₆=29*3
S₆=87
1=2.7*20-53
1=54-53
1=1
ответ: график проходит через точку А