Пусть b1 первый член прогрессии, q знаменатель прогрессии.
По условию задачи сумма бесконечно убывающей геометрической прогрессии 32, то есть:
b1 / (1 - q) = 32. (1)
Сумма первых пяти членов 31, то есть:
b1 * (1 - q^5) / (1 - q) = 31;
(b1 / (1 - q)) * (1 - q^5) = 31; (2)
Заменим первый множитель в левой части уравнения (2) его выражением из (1):
32 * (1 - q^5) = 31;
1 - q^5 = 31/32;
q^5 = 1 - 31/32;
q^5 = 1/32;
q = 1/2.
Подставим значение q в (1) и решим полученное уравнение относительно b1:
b1 / (1 - 1/2) = 32;
b1 = 16.
ответ: 16.
Объяснение:
Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
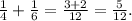
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.
Уравнение прямой имеет вид y=kx+m
k=-7,m=0,т.к. прямая проходит через начало координат.
y=-7x