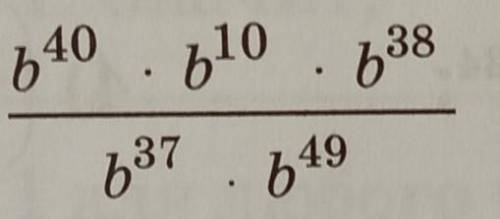
Примем планируемую скорость лыжника за х км/час.
Скорость с которой ехал лыжник реально, будет равна (х + 2) км/час.
Находим время, которое планировалось потратить лыжнику на путь, 15/х ( час)
Находим время, которое потратил лыжник на путь, 15/х+2 (час).
Переводим минуты в часы: 15 мин = 1/4 час.
Составляем уравнение:
15/х - 15/х+2 = 1/4, решаем;
Приводим к общему знаменателю, ищем дополнительные множители, умножаем на них, получаем:
60х + 120 - 60х =х(х+2),
получили квадратное уравнение, находим его корни. Для решения задачи подходит только положительный корень,
х = 10 (км/час) - с такой скоростью планировал ехать лыжник.
10 + 2 = 12 (км/час) - с такой скоростью ехал лыжник.
ответ: 12 км/час скорость лыжника.
Проверка: 15/10 - 15/12 = 1/4 (час).
Объяснение:
1. Верно ли, что уравнение с двумя переменными 6x+7y=12 является линейным?
Да.
Формула линейного уравнения с двумя переменными выглядит так:
ах+ву=с, где х и у -переменные, а,в и с-любые числа.
Данное уравнение 6х+7у=12 соответствует формуле.
2. Верно ли, что уравнение с двумя переменными 2x²-y=0 является линейным?
Нет.
Формула линейного уравнения с двумя переменными выглядит так:
ах+ву=с, где х и у -переменные, а,в и с-любые числа.
Данное уравнение 2х²-у=0 не соответствует формуле.
3. Верно ли, что уравнение с двумя переменными xy-7=9 является линейным?
Нет. Причина выше.
4. Известно, что пара чисел (x; 6) является решением уравнения 3х+7y=63. Найдите значение х.
у=6
Подставляем известное значение у в уравнение и вычисляем х:
3х+7*6=63
3х+42=63
3х=63-42
3х=21
х=7
упростим отдельно числитель и знаменатель:
b^40*b^10*b^38
при умножении степеней с одинаковым основанием, основание остается тем же, а показатели складываются:
b^40+10+38=b^88
b^37*b^49 - все то же самое
b^37+49=b^86
при делении степеней с одинаковым основанием, основание остается тем же, а показатели вычитаются:
b^88:b^86=b^88-86=b^2
подставим значения b
b=8; b^2=8*8=64
b=-1; (-1,3)^2=1,69
b=5/3; 5^2/3^2=25/9= 2 7/9 (две целых и семь девятых)
b=-6; (-6)^2=36
Объяснение: