f(x) = -2x² - x + 5 - квадратичная функция, график - парабола с ветвями, направленными вниз.
I x₀ = -b / (2a) = 1/(-2) = -0,5; y₀ = 5; B(-0,5; 5,25) - вершина параболы
Ось симметрии - прямая x = x₀, то есть в нашем x = -0,5;
Пункт 4) задания мы решили!
II В качестве точек для построения берем:
III Строим график (см. рисунок)
1) При x = -0,3; y ≈ 4,5; при x = 1,2; y ≈ 0,9; при x = 3; y = -16 (здесь проще подставить в функцию...)
2) y = 5 при x = 0 и при x = -0,5; y = 2 при x = 1 и при x = -1,5; y = -1 при x = -2 и при x = 1,5;
3) Нули функции (точки пересечения графика с осью OX)
При x₁ ≈ -1,9 или x₂ ≈ 1,4; y = 0;
Промежутки знакопостоянства:
При x ∈ (-∞; x₁) ∪ (x₂; +∞), f(x) < 0 (x ∈ (-∞; -1,9) ∪ (1,4; +∞))
При x ∈ (x₁; x₂), f(x) > 0 (x ∈ (-1,9; 1,4))
Объяснение:
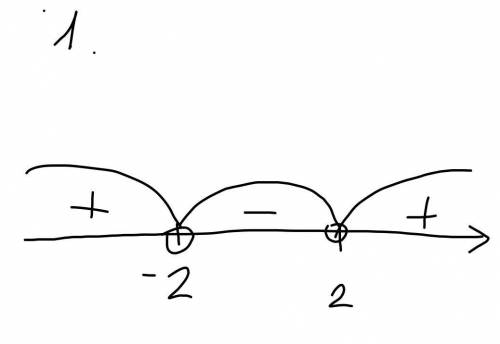
1. x² - 4 > 0
(x-2)(x+2) > 0
x-2=0
x+2=0
x= 2
x= -2
y(1) = 1 - 4 = -3
y(4) = 16 - 4 = 12
x∈ (-∞; -2)∪(2; +∞)
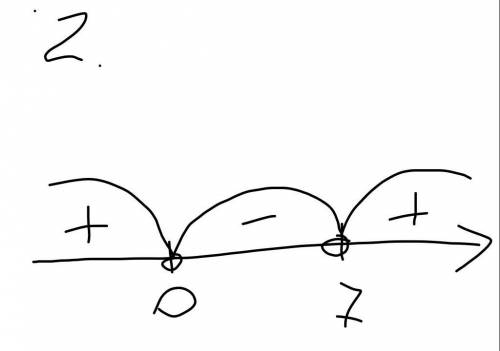
2. x² -7x < 0
x(x-7) < 0
x<0
x - 7 < 0
x < 7
y(2) = 4 - 7*2 = -12
y(9) = 81 - 7*9 = 18
x∈ (0; 7)
3. -3x² +14x - 8 = 0
D= 196 - 4*(-3)*(-8) = 100
√D = 10
x₁ = (-14 + 10)/(-6) = 2/3
x₂ = (-14-10)/(-6) = 4
Тут не нерівність, а рівняння: не вказано більше чи менше 0
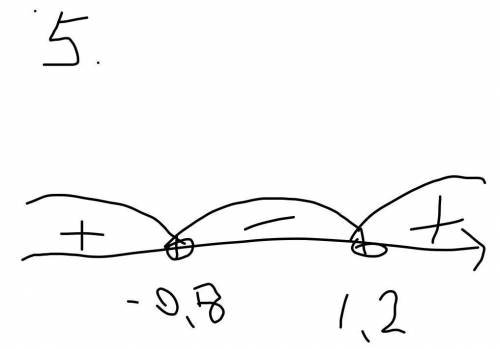
5. x² – 0,4х – 0,96 <0
x² – 0,4х – 0,96 = 0
D = 0.16 -4*(-0.96) = 4
√D = 2
x₁ = (0.4 +2)/2 = 1.2
x₂ = (0.4 -2)/2 = -0.8
y(0) = -0.96
y(2) = 4 - 0.4*2 - 0.96 = 2.24
x∈ (-0.8; 1.2)
3511 заканчивается на 1, при умножении на себя всегда будет давать 1.