См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
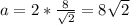 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
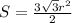 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

1)Находим производную
2)Там, где производная больше 0, там функция возрастает, где меньше 0, там убывает.
Итак, найдём производную:
y' = 3x^2 - 2bx + 3
Функция возрастает на всей числовой прямой, следовательно, чтобы найти значение b, необходим ответить на следующий вопрос: при каком значении b неравенство 3x^2 - 2bx + 3 > 0 выполняется при любом x. Это задача несколько иного плана, останавливаться на ней не буду здесь, решив её, мы получим нужные значения b. Мог бы остановиться на этой задаче, но места не хватит здесь, это задача повышенного уровня сложности и имеет довольно длинное обоснование.