
![acosx-bcos2x1,\\acosx-b(2cos^2x-1)-10,\\\boxed{t:=cosx \Leftrightarrow t \in [-1;1]}\\at-b(2t^2-1)-10,\\2bt^2-at-b+1](/tpl/images/0685/7710/b234d.png)
Переформулируем задачу:
Существуют ли числа a и b, такие, что 2bt² - at - b + 1 < 0 при любом t ∈ [-1; 1]?
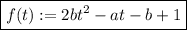
0 ∈ [-1; 1] ⇒ f(0) = 2b·0² - a·0 - b + 1 = 1 - b < 0 ⇔ b > 1.
Тогда при b > 1, график y = f(t) - парабола с ветвями вверх. Значит, решение неравенства f(t) < 0 имеет вид: (t₁; t₂), где t₁, t₂ - корни f(t).
По условию задачи должно выполняться: [-1; 1] ⊂ (t₁; t₂). То есть меньший корень должен быть меньше -1, а больший - больше 1. Для этого необходимо и достаточно, чтобы
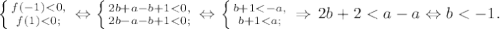
Но, как выяснилось ранее, b > 1 - противоречие.
ответ: нет.
1) 8х + 1,3 = 34,9 - 8х 2) -4 = -2/8х
8х + 8х = 34,9 - 1,3 х = -4 : (-2/8)
16х = 33,6 х = 4 · 8/2
х = 33,6 : 16 х = 2 · 8
х = 2,1 х = 16
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3) 9х = 108 4) 6х - 8 = 6,4
х = 108 : 9 6х = 6,4 + 8
х = 12 6х = 14,4
х = 2,4
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
5) 4(х - 2) = -1 6) 40х = -32
4х - 8 = -1 х = -32 : 40
4х = 8 - 1 х = -0,8
4х = 7
х = 7/4
х = 1 целая 3/4 = 1,75 (в десятичных дробях)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
7) 4х - 2 = 22 8) 5х - 13 + 2(3 - х) = -х + 16
4х = 22 + 2 5х - 13 + 6 - 2х = -х + 16
4х = 24 5х - 2х + х = 16 - 6 + 13
х = 24 : 4 4х = 23
х = 6 х = 23/4 = 5 целых 3/4 = 5,75
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
9) 4(3х + 5) - 3(4х - 1) = 22х + 12
12х + 20 - 12х + 3 = 22х + 12
12х - 12х - 22х = 12 - 3 - 20
-22х = -11
х = -11 : (-22)
х = 1/2 = 0,5 (в десятичных дробях)