Чтобы определить количество корней в квадратном уравнении, достаточно вычислить его дискриминант по формуле: (если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена
Дискриминант больше нуля - два корня
Дискриминант равен нулю. В уравнении 1 корень
Дискриминант меньше нуля, значит нет действительных корней
2)
Найти область определения функции - это найти "проблемные точки" в функции, при которых функция перестанет существовать. В нашем случае, это нельзя допускать, когда знаменатель обратится в ноль. Для этого мы должны его приравнять к нулю и выяснить, при каких значениях функция перестанет существовать.
В нашем случае функция не имеет смысла, при х=-1 и х=0
а)18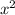 -74
-74
б)-8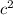 +6c
+6c
в)5х-12
г)1-2а
Объяснение:
а) 2(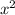 – 3) - 4(17 - 4
– 3) - 4(17 - 4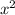 )=2
)=2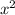 -6-68+16
-6-68+16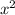 =18
=18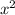 -74
-74
б) c(3-2c) + 3(c-2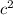 )=3c-2
)=3c-2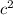 +3c-6
+3c-6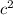 =-8
=-8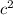 +6c
+6c
в) 4(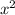 – 3) - x(4x - 5)=4
– 3) - x(4x - 5)=4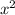 -12-4
-12-4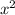 +5х=5х-12
+5х=5х-12
г) 2y - 3 - 2(a + y - 1)=2у-3-2а-2у+2=-1-2а