

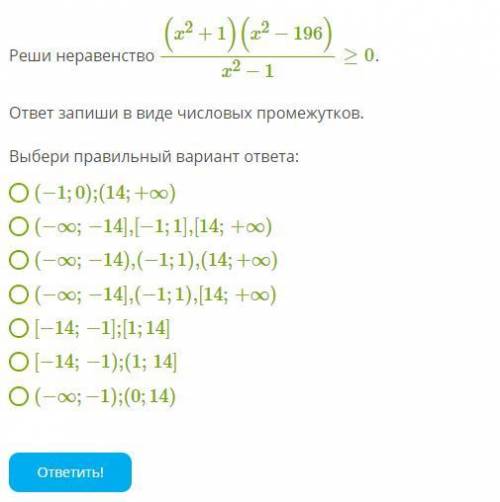
![4)\ \ \dfrac{(x^2+1)(x^2-196)}{x^2-2}\geq 0\ \ \ \Rightarrow \ \ \ \dfrac{(x^2+1)(x-14)(x+14)}{(x-\sqrt2)(x+\sqrt2)}\geq 0\\\\\\znaki:\ \ +++[-14\ ]---(-1\ )+++(\ 1\ )---[\ 14\ ]+++\\\\x\in (-\infty ;-14\ ]\cup (-1\ ;\ 1\ )\cup [\ 14\ ;+\infty \, )](/tpl/images/2032/3179/bc365.png)
a)
*****************************
Квадратное уравнение имеет вид:
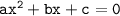
******************************
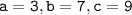
Следовательно уравнение имеет вид:
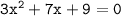
Теперь определим вид данного квадратного уравнения:
Существует 3 вида квадратных уравнений:
имеет 2 корня, если D > 0имеет 1 корень, если D = 0не имеет корней, если D < 0D - дискриминант.
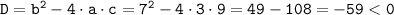 , не имеет корней.
, не имеет корней.
b)
*******************************
Неполное квадратное уравнение, имеющее единственный корень, выглядит следующим образом:
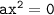 - оно имеет единственный корень,
- оно имеет единственный корень, 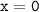
********************************
Пример:
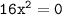
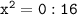
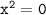
Длина сада 175 м
Ширина сада 140 м
Объяснение:
х - длина сада
у - ширина сада
2,45 га = 24500 (м кв)
По условию задачи периметр сада 630 метров
Система уравнений:
2(х+у)=630
х*у=24500
Во втором уравнении выразим х через у и подставим выражение в первое уравнение:
х=24500/у
2(24500/у)+2у=630
49000/у+2у=630
Избавляемся от дробного выражения, умножаем все части уравнения на у:
49000+2у²=630у
2у²-630у+49000=0/2 делим на 2 для удобства вычислений:
у²-315у+24500=0, квадратное уравнение, ищем корни:
у₁,₂=(315±√99225-98000)/2
у₁,₂=(315±√1225)/2
у₁,₂=(315±35)/2
у₁=140 х₁=24500/140=175
у₂=175 у₂=24500/175=140
Так как по условию х - длина участка, а у - ширина,
решение системы уравнений х=175
у=140
Проверка:
175 * 140 = 24500 (м кв)= 2,45 га
2*(175+140)=630 (м) изгородь сада, периметр. Всё верно.