1. 4x^2 -25=0
D=0+4*25=100
x1=10/8=1,25
x2=-10/8=-1,25
Отрицательный корень уравнения: -1,25
2. Составим пропорцию:
20 кг=(100-84)=16%
х кг=100%
х=20*100/16=125 кг
3. (b+5)x^2+(2b+10)x+4=0
(b+5)x^2+2(b+5)x+4=0
Это квадратное уравнение, а квадратное уравнение имеет один корень, когда дискриминант равен 0(фактически уравнение имеет два равных корня)
найдём дискриминант по формуле для четного коэффициента:
D=(b+5)^2-4(b+5)=b^2+10b+25-4b-20=b^2+6b-5
b^2+6b-5=0
найдём дискриминант по формуле для четного коэффициента:
D=9+5=14
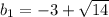
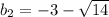
Эти два корня и будут являтся ответом.
Отввет: 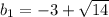 ,
, 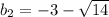
Последнее задание некорректно записано, понять не могу. Отпишитесь в обсуждении или же в Сообщении.
1. 4x^2 -25=0
D=0+4*25=100
x1=10/8=1,25
x2=-10/8=-1,25
Отрицательный корень уравнения: -1,25
2. Составим пропорцию:
20 кг=(100-84)=16%
х кг=100%
х=20*100/16=125 кг
3. (b+5)x^2+(2b+10)x+4=0
(b+5)x^2+2(b+5)x+4=0
Это квадратное уравнение, а квадратное уравнение имеет один корень, когда дискриминант равен 0(фактически уравнение имеет два равных корня)
найдём дискриминант по формуле для четного коэффициента:
D=(b+5)^2-4(b+5)=b^2+10b+25-4b-20=b^2+6b-5
b^2+6b-5=0
найдём дискриминант по формуле для четного коэффициента:
D=9+5=14
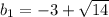
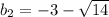
Эти два корня и будут являтся ответом.
Отввет: 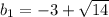 ,
, 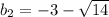
Последнее задание некорректно записано, понять не могу. Отпишитесь в обсуждении или же в Сообщении.
(x+1)(3x+2)(6x+5)^2=1
(3x^2+5x+2)(6x+5)^2=1
(3x^2+5x+2)(36x^2+60x+25)=1
Пусть t=3x^2+5x
тогда уравнение примет вид
(t+2)(12t+25)=1
12t^2+49t+50=1
2t^2+49t+49=0
D=49
t1,2=(-49±7)/(2*12)
t1=-7/3
t2=-1,75
a) 3x^2+5x=-7/3
9x^2+15x+7=0
D=-27<0 - нет решений
б) 3x^2+5x=-1,75
3x^2+5x+1,75=0
12x^2+20x+7=0
D=64
x1,2=(-20±8)/(2*12)
x1=-7/6
x2=-0,5