Вначале заметим, что первообразная скорости равна пройденному пути, откуда имеем следующее:
Для того, чтобы найти путь, пройденной точкой за четвертую секунду, найдем путь, который точка за четыре секунды и за три секунды, а затем из первого вычтем второе.
Считаем разность:
ответ: точка метра за четвертую секунду.
2).
Для нахождения площади этой фигуры можно, во-первых, воспользоваться формулой Ньютона-Лейбница для вычисления интегралов:
В нашем случае (если приравнять и ) .
(как решение уравнения )
(как решение уравнения )
Найдем сам интеграл:
Можно было пойти по-другому: изобразить все на координатной плоскости (смотрите вложенный файл) и по формуле площади прямоугольного треугольника найти площадь :
1) 3sin x = 2 Это даже спрашивать стыдно, простейшее уравнение sin x = 2/3 x = (-1)^n*arcsin(2/3) + pi*k
2) 5sin^2 x + 3sin x*cos x - 3cos^2 x = 2 5sin^2 x + 3sin x*cos x - 3cos^2 x = 2sin^2 x + 2cos^2 x 3sin^2 x + 3sin x*cos x - 5cos^2 x = 0 Делим все на cos^2 x 3tg^2 x + 3tg x - 5 = 0 Квадратное уравнение относительно tg x D = 3^2 + 4*3*5 = 9 + 60 = 69 tg x1 = (-3 - √69)/6; x1 = arctg ( (-3 - √69)/6 ) + pi*k tg x2 = (-3 + √69)/6; x2 = arctg ( (-3 + √69)/6 ) + pi*n
3) 5sin^2 x + √3*sin x*cos x + 6cos^2 x = 5 Решается точно также, как 2), но получается чуть проще 5sin^2 x + √3*sin x*cos x + 6cos^2 x = 5sin^2 x + 5cos^2 x √3*sin x*cos x + cos^2 x = 0 cos x*(√3*sin x + cos x) = 0 cos x1 = 0; x1 = pi/2 + pi*k √3*sin x + cos x = 0 √3*sin x = -cos x tg x2 = -1/√3; x2 = -pi/6 + pi*n
4) sin^2 x = 3cos^2 x + sin 2x sin^2 x - 2sin x*cos x - 3cos^2 x = 0 Дальше опять, как во 2) номере. Делим все на cos^2 x tg^2 x - 2tg x - 3 = 0 (tg x + 1)(tg x - 3) = 0 tg x1 = -1; x1 = -pi/4 + pi*k tg x2 = 3; x2 = arctg 3 + pi*n
Вначале заметим, что первообразная скорости равна пройденному пути, откуда имеем следующее:
Для того, чтобы найти путь, пройденной точкой за четвертую секунду, найдем путь, который точка за четыре секунды и за три секунды, а затем из первого вычтем второе.
Считаем разность:
ответ: точка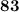
метра за четвертую секунду.
2).Для нахождения площади этой фигуры можно, во-первых, воспользоваться формулой Ньютона-Лейбница для вычисления интегралов:
В нашем случае (если приравнять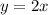
и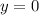 
) 
.
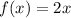Найдем сам интеграл:
Можно было пойти по-другому: изобразить все на координатной плоскости (смотрите вложенный файл) и по формуле площади прямоугольного треугольника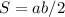
найти площадь 
:
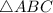В обоих случаях получился одинаковый ответ!
ответ: площадь фигуры равна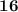
.