![1)\; \; x=-3\; \; ,\; \; y=3,5\\\\(x-3y)^2-(3x-y)^2=\Big [\; A^2-B^2=(A-B)(A+B)\; \Big ]=\\\\=(x-3y-3x+y)(x-3y+3x-y)=(-2x-2y)(4x-4y)=\\\\=-2\cdot 4\cdot (x+y)(x-y)=-8\cdot (-3+3,5)(-3-3,5)=\\\\=-8\cdot 0,5\cdot (-6,5)=26\\\\\\2)\; \; c=-0,05\\\\(c^2-3)^2-(c^2-4)(c^2+2)+4(5-c)^2=\\\\=c^4-6c^2+9-(c^4-2c^2-8)+4(25-10c+c^2)=\\\\=-4c^2+17+100-40c+4c^2=117-40c=117+40\cdot 0,05=119](/tpl/images/0020/3424/f11d5.png)
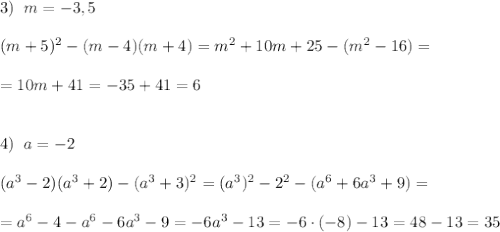
Как добавить хороший ответ
ДОБАВИТЬ СВОЙ ОТВЕТ
Задание
Графіком функції f називають *
геометричну фігуру, яка складається з усіх точок коорди-натної площини, абсциси яких дорівнюють усім значенням аргу-менту, а ординати – відповідним зна-ченням функції f
геометричну фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють усім значенням функції f, а ординати – відпо-відним значенням аргументу
геометричну фігуру, яка складається з усіх точок координатної прямої, абсциси яких дорівнюють усім значенням аргументу, а ординати – вдвічі більші
геометричну фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють значенням функції f
ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)