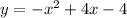

Нужно само решение!
1. Розв'яжіть нерівність sinx >0 :
Відповідь: (2πn; π+2πn), n∊Z
2. cosx >-1/2
Відповідь: (-2π/3+2πn;2π/3+2πn), n∊Z
3. tgx<√3
Відповідь: (-π/2 +πn; π/3+πn)
4. sin2(x) < 1/2 (застосуйте формулу пониження степеня)
Відповідь: (-π/4+πn;π/4+πn), n∊Z
5. 2 sin(x/2 - π/4) ≥ -1
Відповідь: [π/6 + 4πn;17π/6 + 4πn], n∊Z
6. 4sin(x/2)cos(x/2)≤ -1
Відповідь: [-5π/6+2πn;-π/6+2πn], n∊Z
7. sin3xcosx-cos3xsinx ≤ 1/2 (застосуйте формули додавання для тригонометричних функцій)
Відповідь: [-7π/12 + πn;π/12 + πn], n∊Z
Объяснение:
Построим график
Пусть S площадь ограниченная графиком функции осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
Координаты точек A и B:
A(0;-4)
B(2;0)
Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).
Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: .
.
Пусть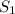 - площадь между прямой
- площадь между прямой 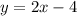 и функцией
и функцией 
Пусть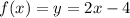 и
и  .
.
По формуле площади прямоугольного треугольника:
Промежуток интегрирования:![[0;2]](/tpl/images/4566/3708/2ae13.png)
Докажем, что при
при ![x \in [0;2]](/tpl/images/4566/3708/4a92d.png)
По теореме: