Question

Известно, что \frac{7x+3y}{x+5y}+\frac{3x-2y}{2x+y}=4
x+5y
7x+3y

+
2x+y
3x−2y

=4

Чему может равняться значение выражения

t=\frac{x^{2}+2y^{2}}{x^{2}-2y^{2}}\ ?
t=
x
2
−2y
2

x
2
+2y
2


?

Если вариантов несколько, запишите в ответ наименьшее возможное значение t.

Answer 1

-3

Объяснение:

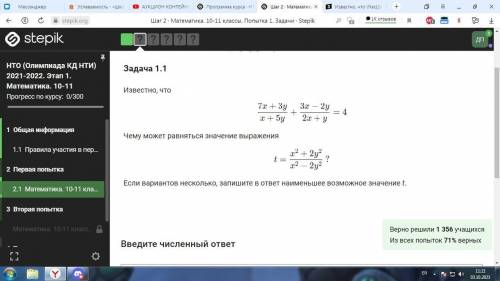
Хорошо, что дали картинку, потому что текстом вы написали полную кашу, в которой ничего непонятно.

(7x+3y)/(x+5y) + (3x-2y)/(2x+y) = 4

Можно попробовать выразить y через x.

Умножим все на (x+5y)(2x+y) и избавимся от дробей.

(7x+3y)(2x+y) + (3x-2y)(x+5y) = 4(x+5y)(2x+y)

14x^2 + 6xy + 7xy + 3y^2 + 3x^2 - 2xy + 15xy - 10y^2 = 8x^2 + 40xy + 4xy + 20y^2

Приводим подобные и собираем все в левой части:

(17-8)x^2 + (13+13-44)xy + (-7-20)y^2 = 0

9x^2 - 18xy - 27y^2 = 0

Делим всё на 9

x^2 - 2xy - 3y^2 = 0

Делим всё на y^2

(x/y)^2 - 2(x/y) - 3 = 0

Обозначим x/y = n

n^2 - 2n - 3 = 0

(n+1)(n-3) = 0

1) n = x/y = -1; x = -y; x^2 = y^2, тогда:

t = (x^2 + 2y^2)/(x^2 - 2y^2) = 3y^2/(-y^2) = -3

2) n = x/y = 3; x = 3y; x^2 = 9y^2, тогда:

t = (x^2 + 2y^2)/(x^2 - 2y^2) = 11y^2/(7y^2) = 11/7

Наименьшее из чисел (-3; 11/7) = -3