В решении.
Объяснение:
Найти:
1) D(y);
Область определения - это значения х, при которых функция существует, или это проекция графика функции на ось Ох.
Обозначается как D(f) или D(у).
Согласно графика, D(у) = [-6; 6];
2) E(y);
Область значений - это значения у, в каких пределах функция существует, или это проекция графика на ось Оу.
Обозначается как Е(f) или Е(y).
Согласно графика, Е(y) = [0; 4];
3) Нули функции - точки пересечения графиком оси Ох, где у = 0.
Согласно графика, точка (0; 0) - нуль данной функции.
4) Монотонность функции.
Функция возрастает на промежутках х∈[-6; -3] и х∈[0; 3];
Функция убывает на промежутках х∈[-3; 0] и х∈[3; 6].
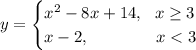
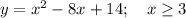
Найдём вершину параболы:
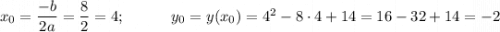
В данной точке можно обозначить опорную прямую, которая будет симметрична для ветвей (тогда значения с одной стороны можно просто симметрично перенести на другую)
Возьмём 3 точки (при ограничении прямой x < 3 даже 3-ёх много будет)
1) x = 5
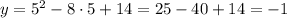
2) x = 6
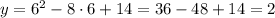
3) x = 7
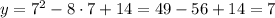
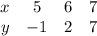
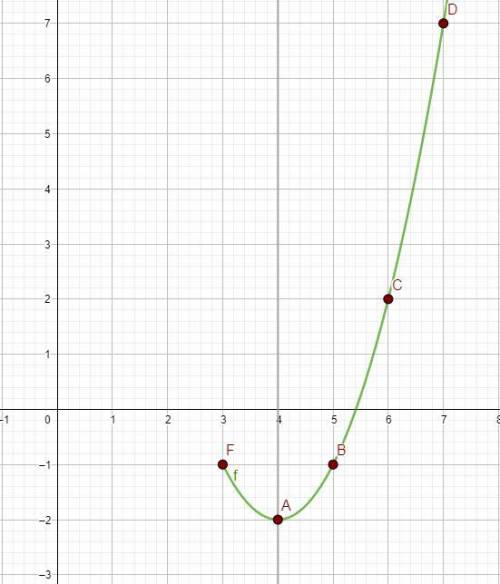
Отмечаем точки на координатной плоскости и симметрично их копируем относительно вс прямой
Не стоит забывать что условие ограничения функции x ≥ 3, поэтому переносим только точку, симметричную B; позже на графике эта точка будет закрашена и обозначена как A
(картинка 1)
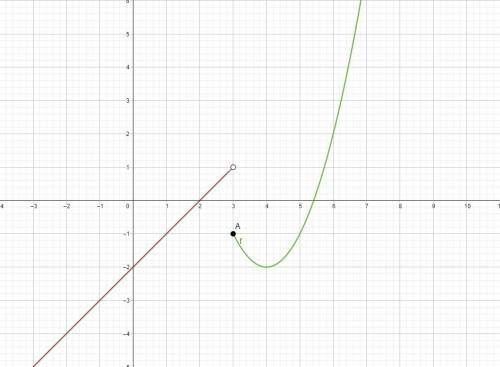
Разбираемся со вторым графиком
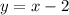
Уравнение прямой, достаточно двух точек
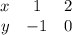
Условие x < 3, точка (3; 1) выколота
(картинка 2)
y = m
При m = 1 (и всё что выше) получаем 1 точку пересечения
Следовательно, подходят все значения до m = 1
При m = -1 и до m = -2 имеем 3 точки пересечения
При m = -2 2 точки пересечения (вершина параболы и прямая)
Следовательно нам подходят значения -2; от -1 до 1 не включительно
ответ: 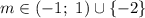
Если перед скобками стоит знак минус, то знаки в скобках меняются на противоположные.
Упростим выражение в правой части равенства. Для этого раскроем скобки и приведём подобные слагаемые:
= 4,2х - 8,4у - 4у - 4,2х + 8,4у + 5х = (4,2х - 4,2х + 5х) - (8,4у + 4у - 8,4у) =
= 5х - 4у.
Это тождество, так как левая часть выражения равна правой.