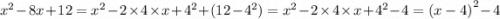В решении.
Объяснение:
Решить графически систему уравнений:
у = 9 - х
у = х - 1
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 9 - х у = х - 1
Таблицы:
х -1 0 1 х -1 0 1
у 10 9 8 у -2 -1 0
Координаты точки пересечения прямых: (5; 4).
Решение системы уравнений: (5; 4).
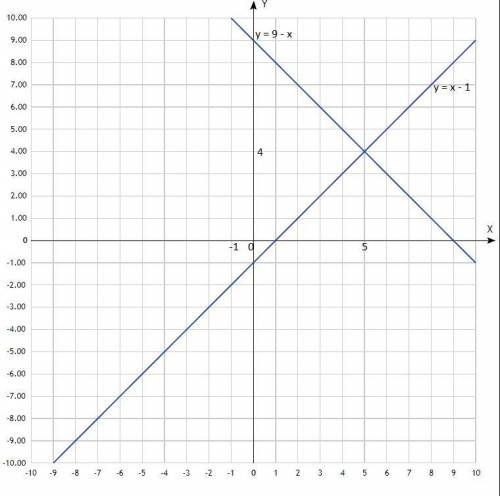
1) не является; 2) не является
Объяснение:
1) Является ли у функцией х, если у - это число десятых в десятичной записи числа х?
У некоторых чисел существует 2 формы десятичной записи: с 0 и с 9 в периоде.
Например, для числа 1 существуют 2 формы:  и
и 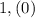 . В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной
. В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной 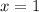 , которому соответствуют несколько значений
, которому соответствуют несколько значений 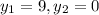 .
.
Значит, у не является функцией х.
2) Является ли x функцией y, если у - это число десятых в десятичной записи числа х?
Рассмотрим 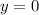 . Но число десятых у чисел
. Но число десятых у чисел  и
и 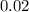 равно нулю. То есть существует значение переменной
равно нулю. То есть существует значение переменной 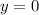 , которому соответствуют несколько значений
, которому соответствуют несколько значений  (например,
(например, 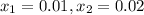 ).
).
Значит, x не является функцией y.
#1. Функция задана формулой
1.1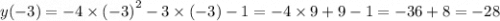
1.2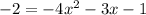
1.3 x = - 1, y = - 2, подставляем значения в функцию, если равенство будет верным, то значит точка А(-1; - 2) принадлежит графику функции. (в 1.2 мы нашли корни уравнения, при y=-2, x=-1, значит точка принадлежит графику функции, но, всё же, распишу так: )
равенство верное, точка принадлежит графику функции.
#2. Используя график функции укажите:
2.1 Область определения функции: [-4.5; 5]
2.2 Область значения функции: [-2.5; 4.5]
2.3 Промежутки возрастания функции: [-4.5; 1], промежутки убывания функции: [1; 5]
#3.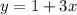 .
.
Это линейная функция, формула которой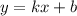 , где
, где
если k > 0, то функция возрастающая, если k < 0, то функция убывающая.
У нас k = 3, 3 > 0 => функция возрастающая.
#4. Найти область определения функции:
4.1
Область определения:
4.2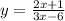
знаменатель не должен быть равным нулю: ,
, 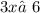 ,
, 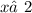
Область определения: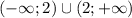
4.3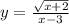
в числителе корень, число под корнем не должно быть отрицательным: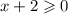 ,
, 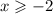
знаменатель не должен быть равным нулю: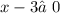 ,
, 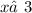
Область определения: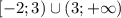
4.4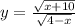
в числителе корень, число под корнем не должно быть отрицательным: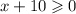 ,
, 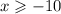
в знаменателе корень, число под корнем не должно быть отрицательным; знаменатель не должен быть равным нулю: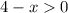 ,
, 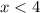
Область определения: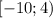
#5. Разложить на множители квадратный трёхчлен. Можно это сделать по формуле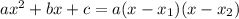 , где
, где 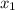 и
и 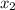 — корни уравнения
— корни уравнения 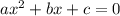 .
.
5.1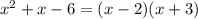
5.2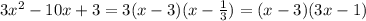
#6. Найти значение дроби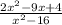 при
при  .
.
Для начала нужно упростить дробь.
Разложим квадратный трёхчлен из числителя на множители, по формуле из задания 5.
В знаменателе разность квадратов, используем формулу сокращенного умножения.
В итоге,
#7. а)