ответ:
y' = 4x^3-4x
приравниваем ее к нулю:
4x^3-4x = 0
x1 = 0
x2 = -1
x3 = 1
вычисляем значения функции
f(0) = 8
f(-1) = 7
f(1) = 7
fmin = 7, fmax = 8
используем достаточное условие экстремума функции одной переменной. найдем вторую производную:
y'' = 12x^2-4
вычисляем:
y''(0) = -4< 0 - значит точка x = 0 точка максимума функции.
y''(-1) = 8> 0 - значит точка x = -1 точка минимума функции.
y''(1) = 8> 0 - значит точка x = 1 точка минимума функции.
объяснение:
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
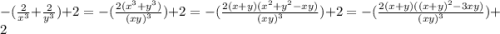
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
7,0×5y6 будет гарантия не даю