а)так как прямая долна проходить через начало координат, то ее уравнение имеет вид:
у=кх
Подставляем координаты точки А(0,6;-2,4) через которую она проходит в уравнение, получаем: -2,4=0,6к
к=-2,4:0,6
к=-4
Значит уравнение прямой имеет вид : у=-4х
б)так как прямая пересекает оси в двух точках, то ее уравнение имеет вид:
у=kx+b
Подставляем координаты точки В(0; 4) в уравнение у=kx+b и получаем :
4=b
Подставляем координаты точки С(-2,5; 0) в уравнение у=kx+b и 4=b, получаем
0=-2,5к+4. Решаем:
-4=-2,5к
к=(-4):(-2,5)
к= 40/25=8/5=1,6
Значит уравнение прямой имеет вид: у=1,6х+4
Кусочно- заданная функция - это функция , которая на различных промежутках оси ОХ задаётся разными функциями. ( Как бы на разных "кусочках" оси ОХ задаются разные функции).
На промежутке (-∞ ; -2 ] функция представляет из себя гиперболу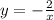
. График гиперболы рисуем только на этом промежутке (сплошной линией), оставшаяся часть графика на промежутке (-2 ; +∞) стирается (либо рисуется пунктирной линией). Точка с абсциссой х= -2 , точка (-2,1) , принадлежит этому графику.
На промежутке (-2 ; 2] рисуем график у=|x|-1 . Это график функции у=|x|, который смещён на 1 единицу вниз по оси ОУ. Точка (-2,1) не принадлежит графику, а точка (2, 1) принадлежит графику.
На промежутке (2 ; + ∞) рисуем график функции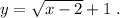
Это график функции 
, смещённый вдоль оси ОХ на 2 единицы вправо и вдоль оси ОУ на 1 единицу вверх . Точка (2,1) не принадлежит графику функции.
График кусочно заданной функции нарисован сплошными линиями.