В теории чисел (делимость и сравнение по модулю) доказывается, что остатки от деления повторяются с некоторым периодом.
В данной задаче остатки от деления числа 3^n на 7 при увеличении n повторяются с периодом 6:
первое число, при делении на 7 дающее в остатке 5, это число 243 (при n=5), следующее 177147 (при n=11) и т.д.
Подробнее:
n=5 3^n=243=34*7+5
n=11 3^n=177147=25306*7+5
n=17 3^n=...
n=23 3^n=...
...
Можем записать
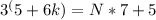
где k=0,1,2,3,4,...
По условию задачи n-двузначное число, следовательно
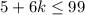
отсюда максимально возможное значение k=15
n=5+6*15=95
ответ: наибольшее двузначное число n=95
Объяснение:
a) 2^12 *2² /62=2^14/2*31²= 2^14/2²*31²= 2^12/31²=4096/961= =4 252/961
б)8^4*49^4 / 147 =(2^3)^4 *(7^2)^4 /3*49=2^12*7^8/3*7²= =2^12*7^6 / 3= 4096*117649/ 3= 481890304/ 3=160630101 1/3